Esta práctica es relativamente nueva, la idea es estudiar mecanismos con lazo de control realimentado para regular un proceso variable y mantenerlo en un punto de trabajo seleccionado. El experimento propuesto específico consiste en mantener la posición vertical de un flotante en un fluido en movimiento (controlando el flujo/caudal de este fluido).
Para el análisis y la comprensión de este tipo de técnica de instrumentación, se parte de suponer que los sistemas que se pretenden controlar son lineales e invariantes en el tiempo, Estas dos condiciones implican: la primera, que en el problema vale el principio de superposición, y que no se crean frecuencias nuevas. Dado un impulso el sistema responde en forma lineal: el sistema mapea en forma lineal la entrada a la salida. La segunda condición implica que la salida no depende del tiempo en el que la perturbación fue aplicada. La respuesta, o salida $y(t)$ de estos sistemas, dado un estímulo de entrada $x(t)$ se obtiene a partir de la operación de convolución:
$y(t)=(h*x)t=\int_{-\infty}^{\infty}h(\tau)x(t-\tau)d\tau$,
donde $h(t)$ es lo que se llama la función de respuesta del sistema, o respuesta al impulso. Para esta clase de sistemas, una herramienta muy útil es la transformada de Laplace: una transformación parecida a la transformada de Fourier. La transformada de Laplace de una función en el dominio del tiempo $f(t)$ es
$F(s)=\int_0^{\infty}f(t)e^{-st}dt$
En el espacio transformado de la variable compleja $s$ (que tiene unidades de frecuencia), la respuesta $Y(s)$ del sistema lineal e invariante temporal $H(s)$ a una perturbación $X(s)$ es el producto $Y(s)=H(s)X(s)$.
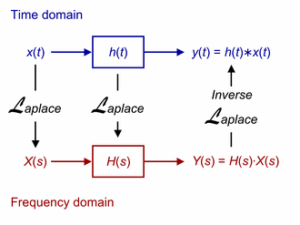
Entonces, trabajando en el espacio transformado (Laplace) en un sistema sin realimentación, puedo obtener la respuesta o función de transferencia del sistema:
$H(s)=Y(s)/X(s)$ .
Ahora imaginemos que precisamos controlar “perfectamente” la salida del sistema, es decir queremos que su estado sea fijo, o controlado, digamos, y que sea siempre el mismo independientemente de las condiciones externas. Por ejemplo esto sería como pretender que el interior de la heladera esté siempre a la misma temperatura (considerablemente más baja que la del exterior) independientemente de si es un día frío o un día caluroso. O, en un vehículo, poder mantener una velocidad constante independientemente de si el terreno tiene pendiente ascendente, descendente, o es plano. Esta es la idea de los dispositivos de control. Usualmente nosotros aplicamos alguna señal de entrada y el sistema responde llegando a un estado estacionario, que puede variar día a día. Queremos agregarle “algo” al sistema de interés, de forma tal que nosotros sólo tengamos que aplicar como entrada un valor de seteo o deseado (lo llamamos $SP$, setpoint), y que la salida del sistema así controlado por ese “algo”, $Y$, copie al setpoint. Es decir, $SP-Y=0$.
Entonces, copiando la estructura de la parte “roja” de la figura de arriba tenemos el siguiente esquema, que incluye al sistema: $H$; al “algo”: $K$ (el controlador); y una etapa que compara la señal de entrada (seteo, $SP$) con la salida $Y$:
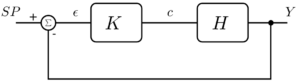
Aquí, el “usuario” define el setpoint $SP$, que es lo que pretende que sea la salida del sistema. Sobre el sistema $H$ ya no se actúa directamente como antes, sino que el controlador $K$ es quien define la señal de control $c$, usando como premisa que el error $\epsilon$, es decir la diferencia entre el setpoint y la salida, sea 0. Pensandolo como en la parte anterior, en el espacio de Laplace, la salida es
$Y(s)=\epsilon(s) K(s) H(s)=(SP(s)-Y(s)) K(s) H(s)$.
A $K(s)$ se la denomina la función de transferencia del controlador, mientras que la función de transferencia del circuito cerrado se obtiene reacomodando la expresión anterior y es:
$\frac{Y}{SP}=\frac{K\,H}{1+K\,H}$.
$K$ puede ser un dispositivo o un protocolo muy sofisticado, o puede ser algo simple. El controlador de lazo cerrado más común es el que genera un estímulo $c$ combinando una señal proporcional al error $\epsilon$ (P), otra igual a la integral de $\epsilon$ (I) y otra igual a la derivada (D): de ahí su nombre PID. Cuál es el peso o la proporción en la aparecen cada uno de estos tres términos para lograr un “buen” control del sistema? ésta es una tarea delicada, que depende de cada sistema. Por control “bueno” se entiende uno que haga que el sistema llegue al punto de seteo en un tiempo corto, que no oscile, que durante el transitorio no realice excursiones a valores no deseados de la salida, entre otras cualidades.
La práctica consiste en familiarizarse con este tipo de procesos, tratar de obtener los parámetros óptimos del controlador, y (a veces, cuando se puede) tratar de inferirlos conociendo la dinámica del sistema $H$. Esto último NO SIEMPRE ocurre. Además, como siempre, en la práctica aparecen otro tipo de técnicas de instrumentación, en particular en lo que tiene que ver con la medición de la “salida” del sistema, y la determinación de la señal de error. Lo importante es distinguir las distintas etapas de la práctica.
Material de referencia del tema (en orden):
- Lectura introductoria
- Un tutorial sobre control PID de Matlab: https://www.mathworks.com/videos/understanding-pid-control-part-1-what-is-pid-control–1527089264373.html
- Una introducción al uso de la transformada de Laplace para diseño de control PID, (con ejemplos!).
- Colab con simulaciones usando transformada de Laplace (por Marcelo Luda)
- PID. Preguntas para responder
- Códigos Python específicos para el experimento
Redursos adicionales
- Página de National Instrument sobre controladores PID: http://www.ni.com/es-cr/innovations/white-papers/06/pid-theory-explained.html
- Implementación de un lazo PID en controladores de temperatura.
- Método de sintonización de Ziegler-Nichols
