Hola, parte de la clase mañana iba a estar dedicada a mostrarles brevemente como hacer una simulación 3D usando Vpython. Es algo completamente extra para introducirlos a la simulación, asi que queda en el interés de cada uno interiorizarse y aprender más.

Vpython es una librería de Python, se puede importar si ya tienen instalado Python. Pero también pueden correrlo online creándose una cuenta en https://www.glowscript.org/, lo cual lo hace super accesible para empezar.
En la página pueden ver documentación de ayuda y programas ejemplo. En la página de Youtube de Javier Carro hay más tutoriales.
Los programas ajenos no se pueden editar: hay que copiarlos y pegarlos en uno propio que creemos.
El código es muy intuitivo: solo con sphere() ya pueden crean una esfera: ualá!
En el siguiente código hay ejemplos de como crear distintas figuras. Prueben ir comentado y descomentando (con #) las líneas una a una.
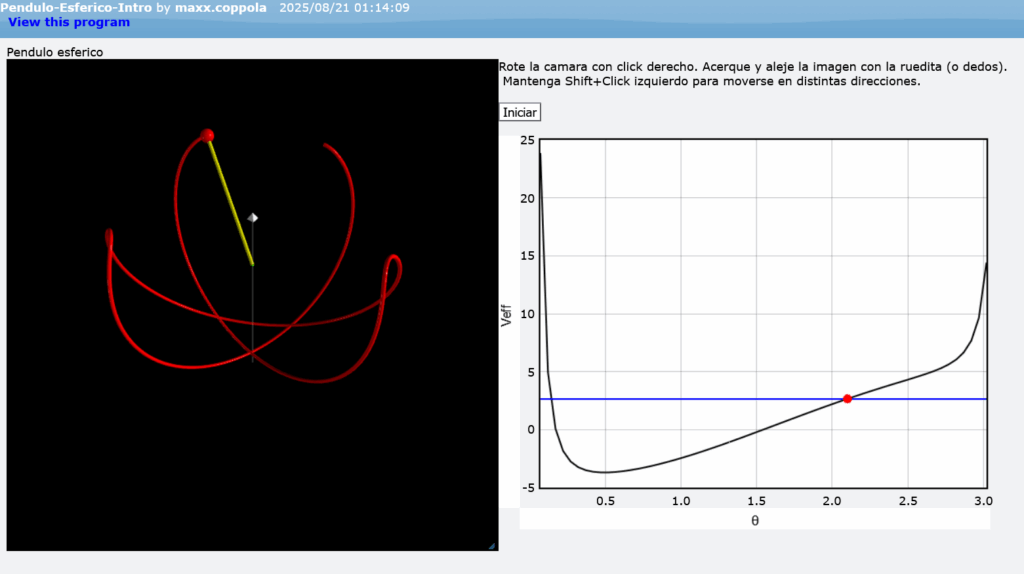
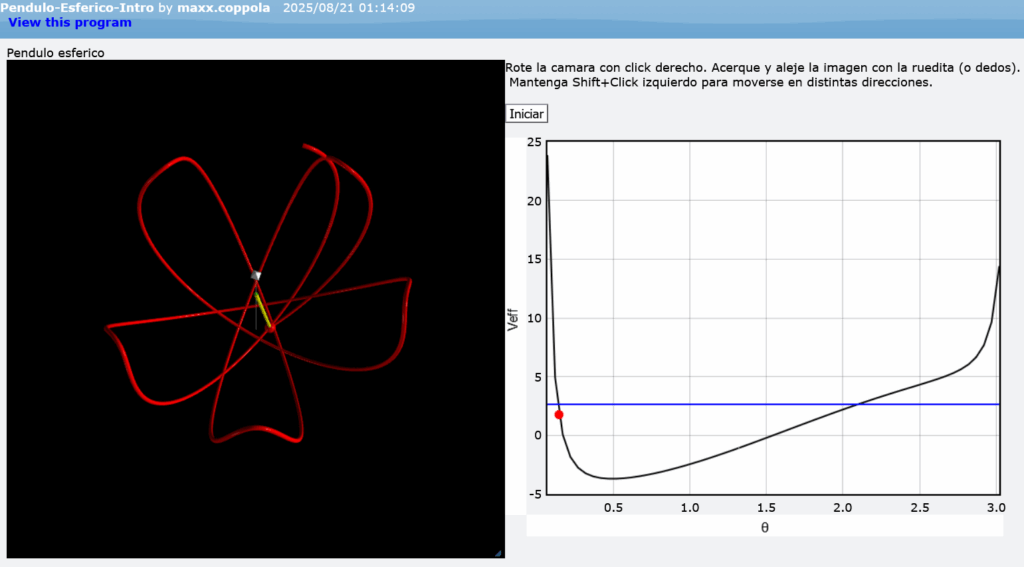
Vamos a simular el péndulo esférico: aquí una resolución teórica del problema. Y aquí la simulación.
Dejé varias condiciones iguales para que prueben.
También hay un gráfico del potencial efectivo, con un punto rojo que indica la posición del péndulo.
Deje varias explicaciones en cada línea, prueben a ver si pueden seguirlo.
La posición del péndulo viene dada por las ecuaciones de movimiento. Existen muchos métodos para integrarlas numéricamente. El más simple es el método de Euler de un paso. La idea es simple: aproximar una curva por su tangente. Hacemos esto muchas veces en intervalos dx. Cuanto más pequeño sea dx, más curvas tangentes usamos y mejor sera la aproximación, pero más lento será el codigo. Creo que una imagen lo explica mejor:

La idea es partir del punto inicial que es conocido. En cada punto siguiente aproximamos la función a primer orden: f(x+dx)~f(x)+f'(x)dx. Como estamos solo a primer orden, la precisión no es muy buena.

Si miran el código, al final (dentro del while) se actualiza la posición del péndulo haciendo un Taylor a primer orden de la posición y la velocidad, donde la aceleración está evaluada en el punto anterior usando las ecuaciones de movimiento del péndulo.
Anímense a probar ustedes! Empiecen sacando el gráfico del potencial efectivo para reducir complejidad.

Deja un comentario