Física 2 – Depine

Autor: Ricardo Angel Depine

  • El problema del martes pasado

    Antes que nada: mañana no habrá clases teóricas ni prácticas.

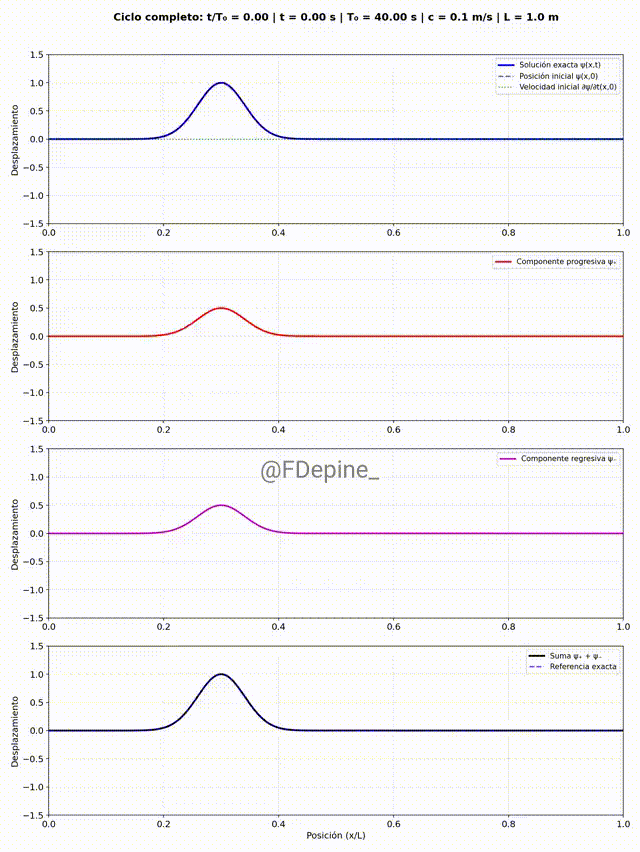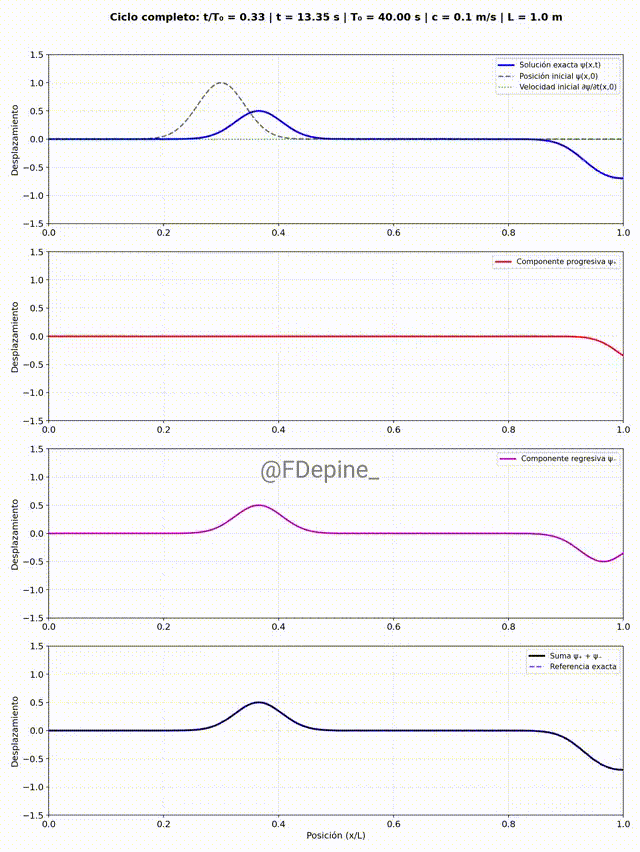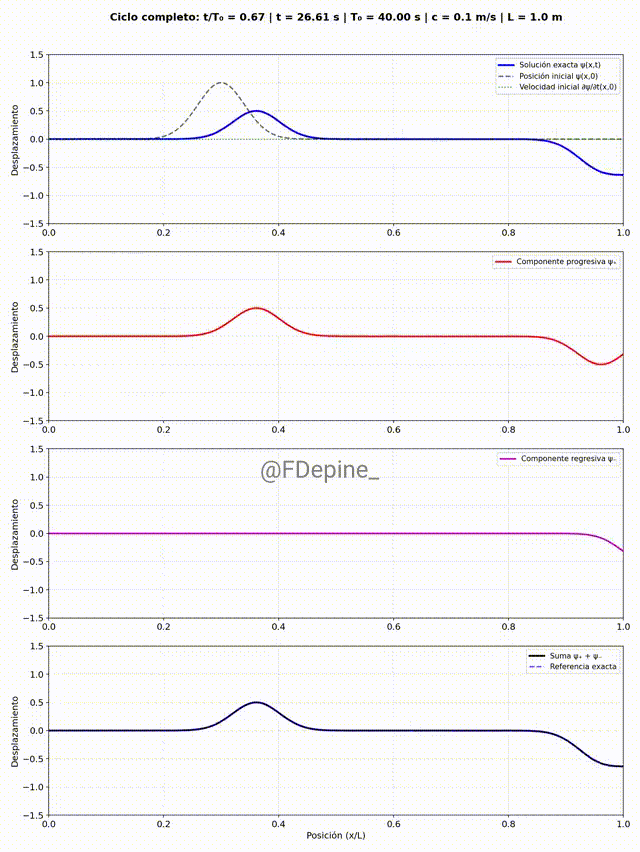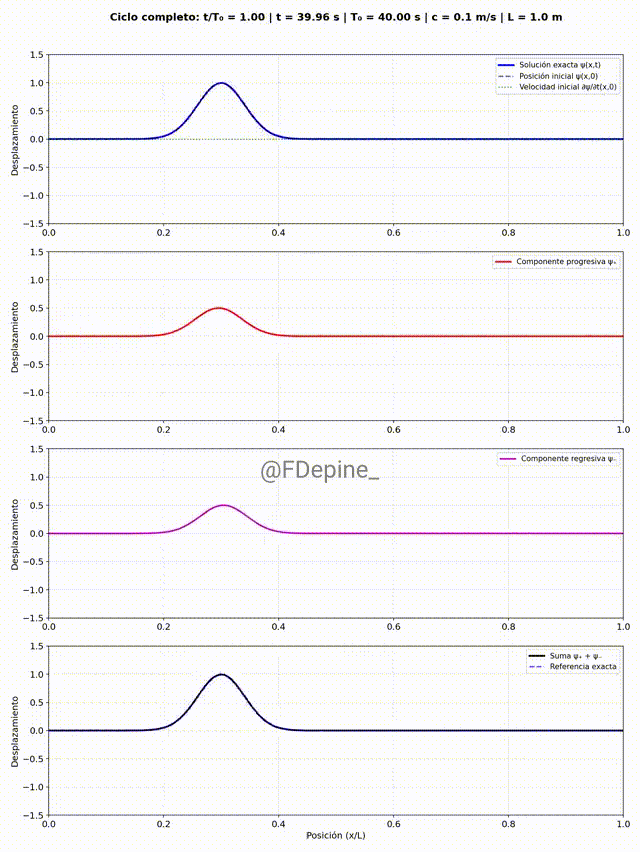
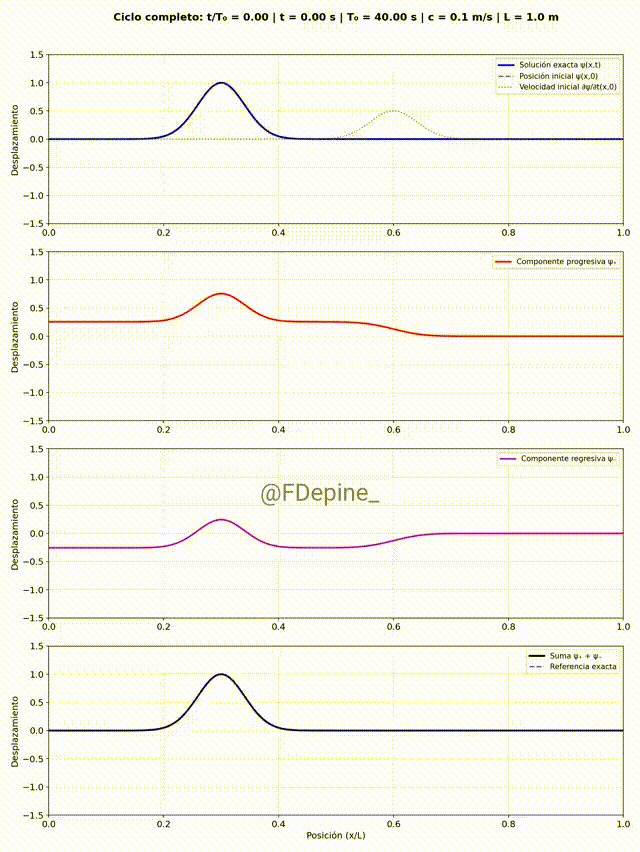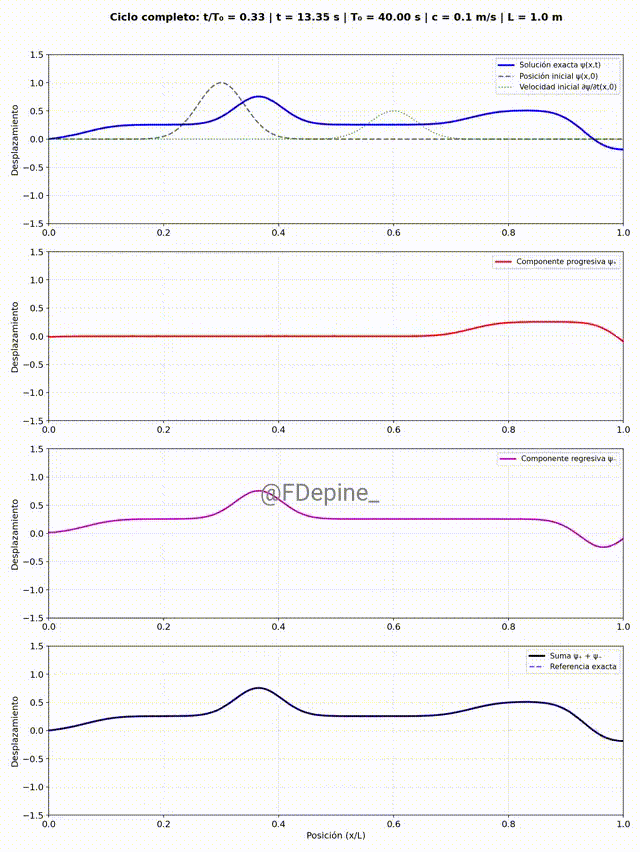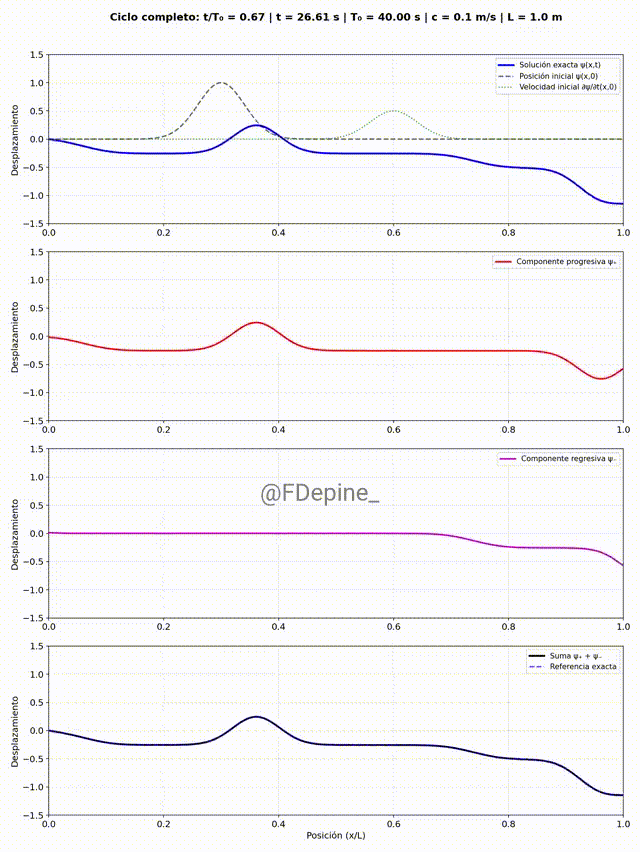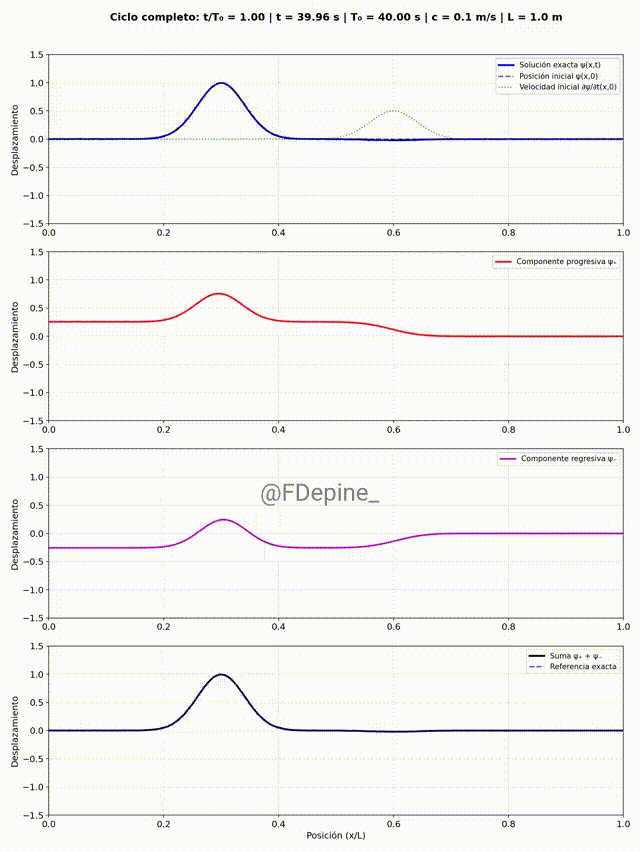
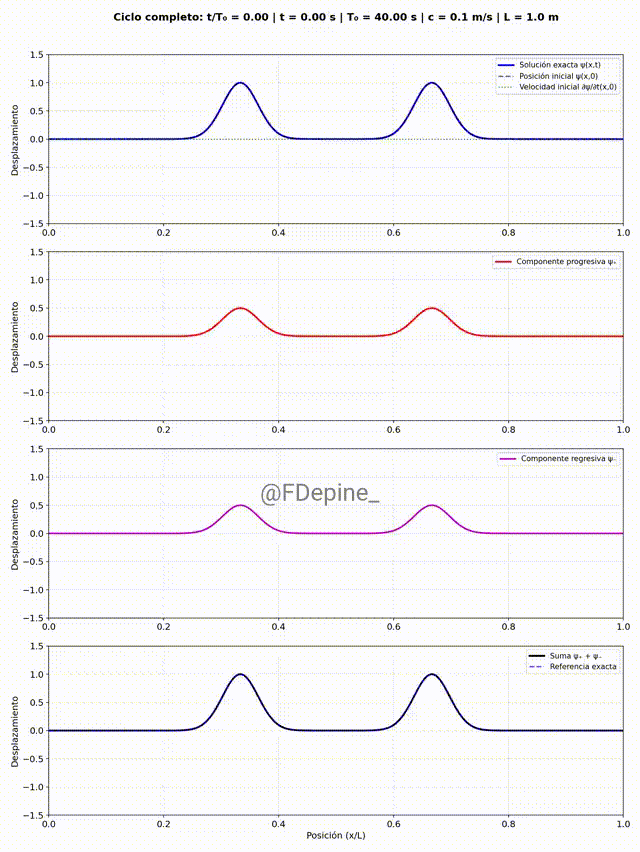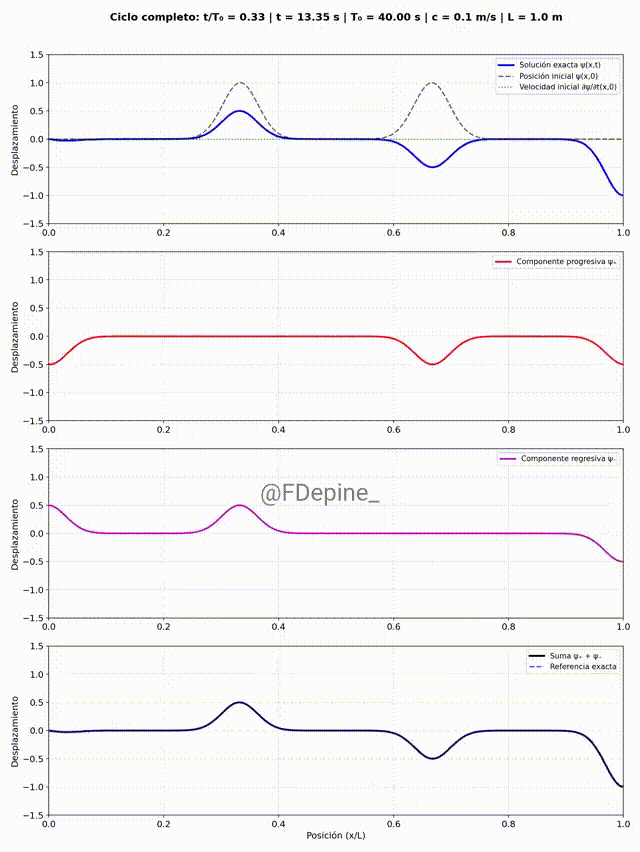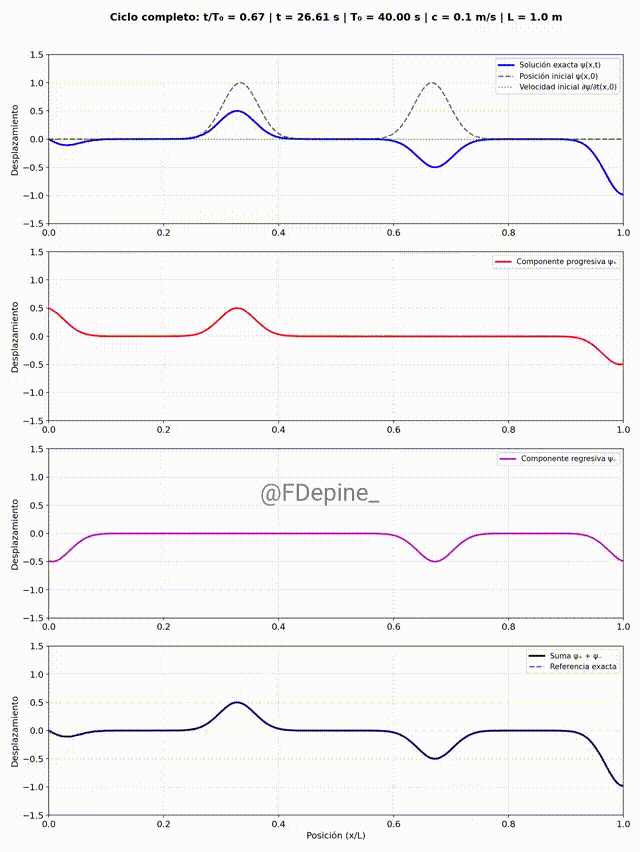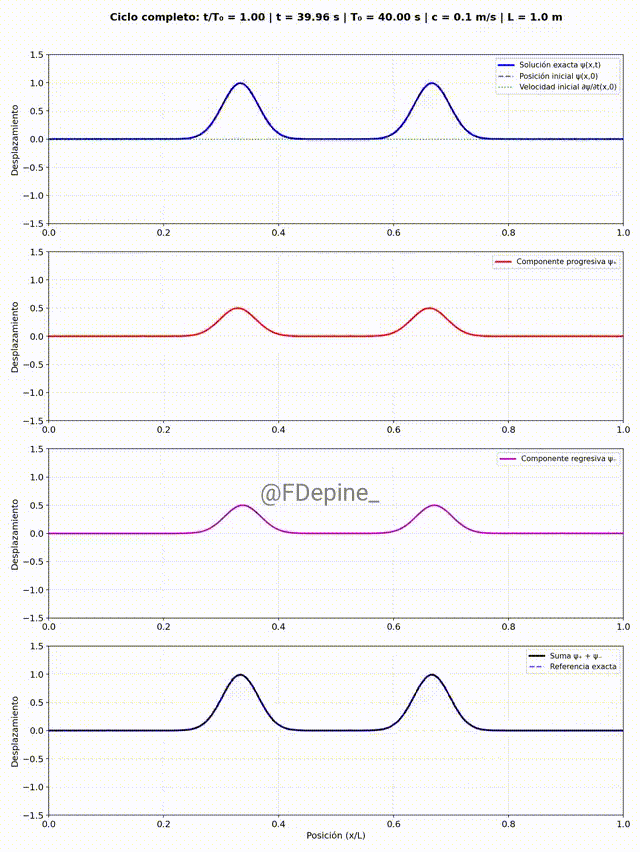
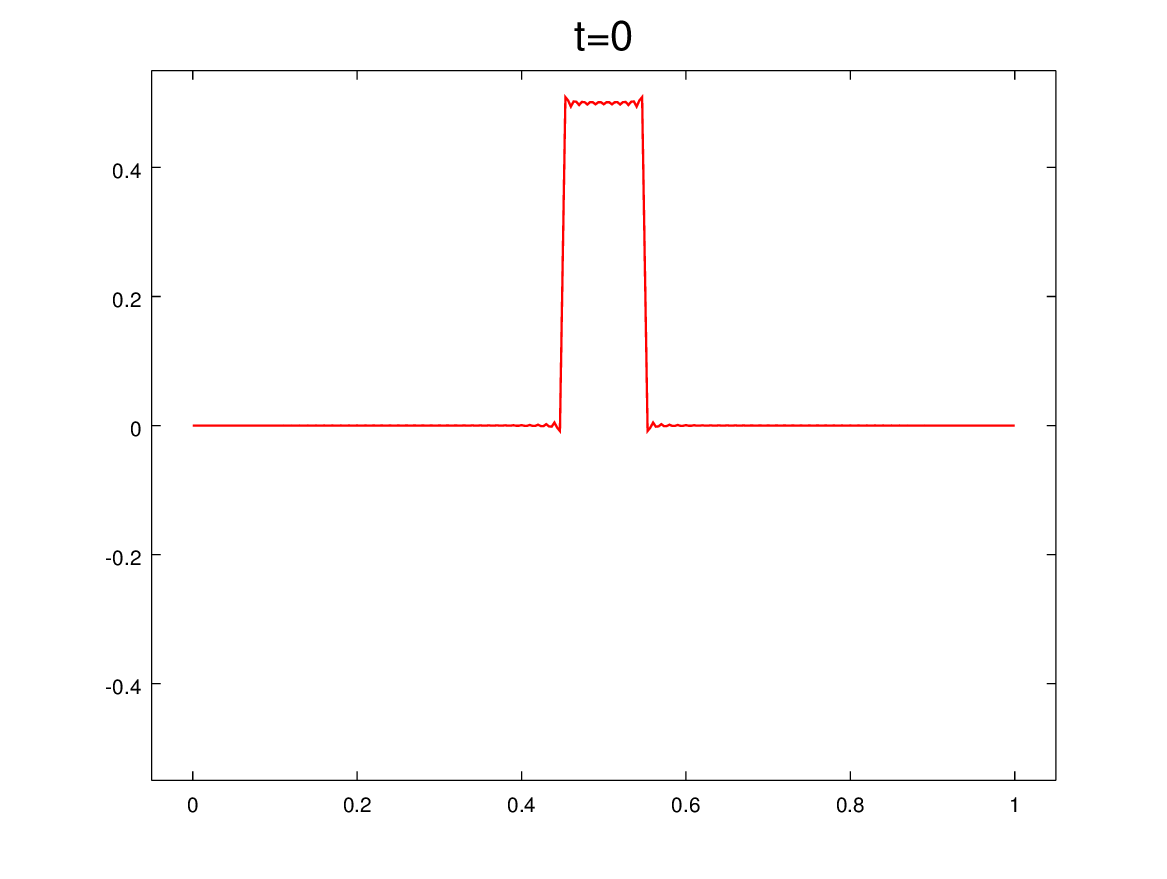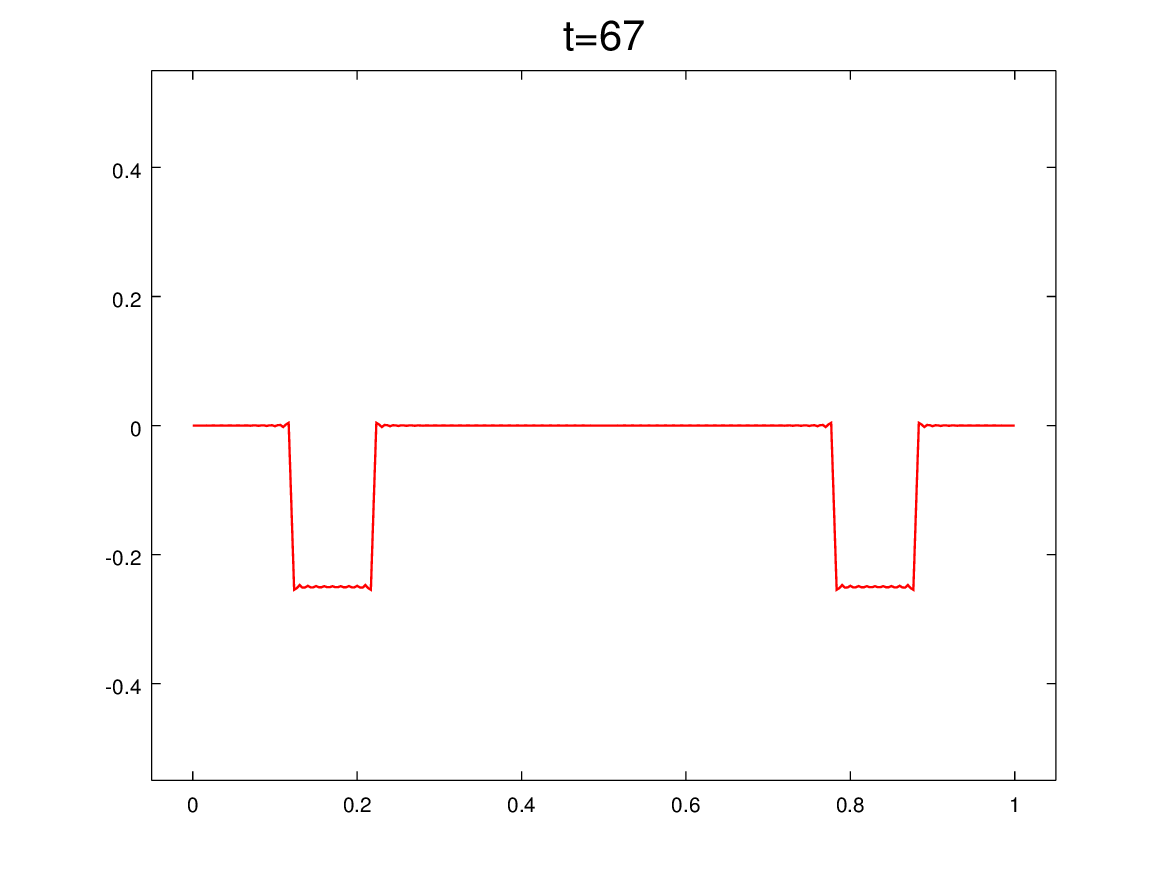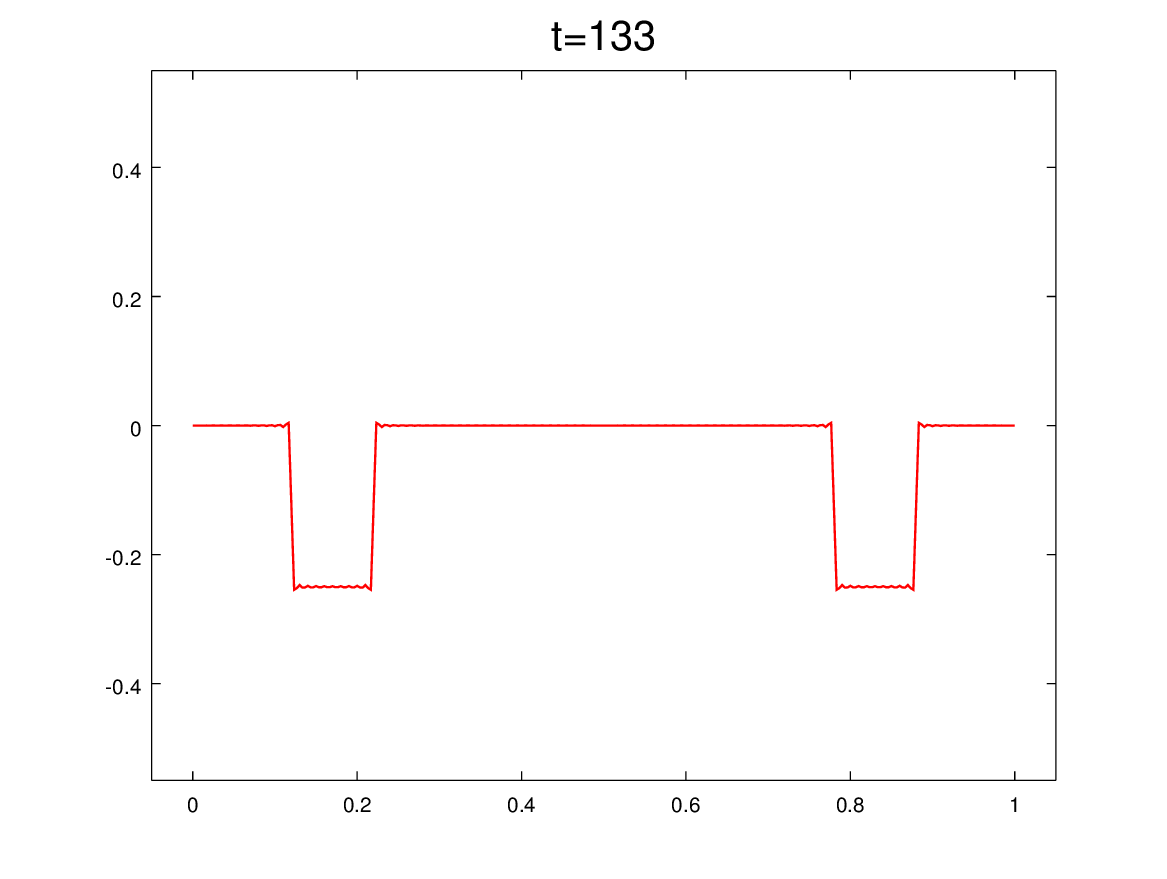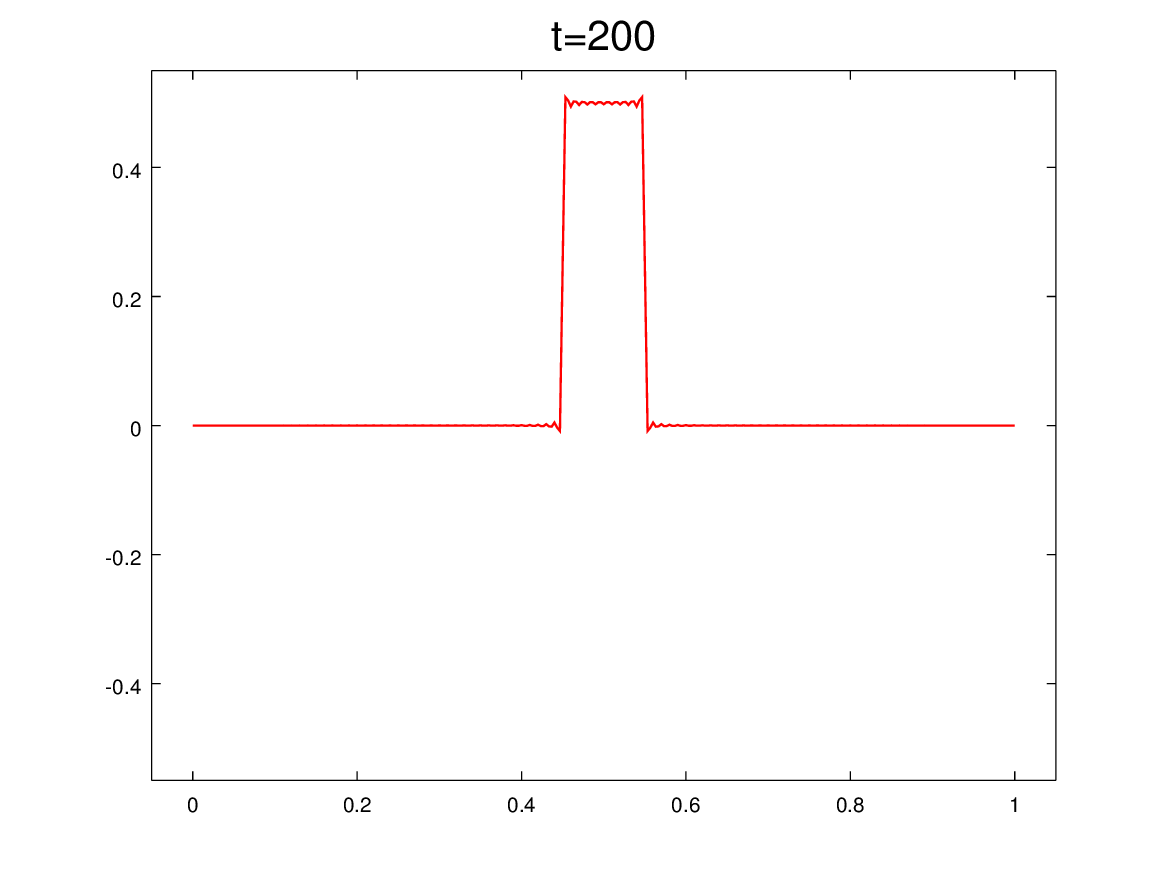
    Y para mitigar las nostalgias provocadas por las no clases del viernes 2 y de mañana, les dejo algunos comentarios sobre el problema que vimos el martes 29/4, que pone en evidencia cómo tratar problemas ondulatorios cuando hay discontinuidades en el medio. En nuestro caso, el medio era la soga y la discontinuidad estaba en el medio del medio (en x=L/2).

    Este problema está tratado en el Capítulo VI del volumen 1 del libro “The Theory of Sound” (1877) de Lord Rayleigh.

    donde primero discute el caso más general, de la masa M en cualquier posición, y luego especializa los resultados para el caso x=L/2

    (ampliar imàgenes abriendo en otra pestaña, libro disponible en Internet Archive).

    Contexto histórico:

    • John William Strutt (Lord Rayleigh): Físico británico (1842–1919), Nobel de Física 1904, pionero en acústica, teoría de vibraciones y scattering.
    • Su trabajo unificó matemáticas avanzadas con aplicaciones prácticas (por lo general en todas las áreas de la física siempre hay algo llamado “de Rayleigh”).

    Importancia de leer trabajos originales

    • Comparar la derivación de Rayleigh con los libros de texto modernos.
    • Los originales revelan el proceso creativo (errores, intuiciones físicas).
    • Observar cómo Rayleigh usó argumentos físicos (energía, simetría) junto a matemáticas rigurosas.

    Analogías modernas del problema: muchas, entre ellas:

    • Física cuántica: Una masa puntual en una cuerda es análoga a un átomo en un potencial periódico (modelos de defectos en sólidos).
    • Ingeniería: Cables con sensores (masas discretas) para monitorear vibraciones en puentes.
    • Acústica: los defectos producen modos normales alterados (se usa para fabricar instrumentos musicales y para el diseño de altavoces).

    Actividad propuesta

    1. Leer las páginas 161–163 de The Theory of Sound.
    2. Comparar la solución de Rayleigh con la obtenida en clase.

  • Condición de borde de impedancia

    Hay problemas físicos donde la condición de borde (o de extremo en el caso 1D) no se expresa ni fijando el valor de la función (caso de soga con extremo fijo) ni el valor de la derivada (extremo libre sin masa). Por ejemplo, para una soga con una masa M en el extremo derecho, la condición de borde se puede escribir como una proporcionalidad entre la función y su derivada en en x=L. Estas condiciones que mezclan función y derivada se conocen en algunas áreas de la física como condiciones de borde de Robin y en otras como condiciones de impedancia.

    Notar que si el extremo izquierdo en x=0 está fijo, los modos siguen siendo funciones sinusoidales de kx (lo mismo que cuando M era 0). Pero con una diferencia: los valores del k adimensional K=kL ya no son raíces del coseno (la derivada del seno), sino que son raíces de la ecuación trascendente

    F(K) = cos K + K P sen (K)

    donde el parámetro adimensional P = M / (ρ L) es el cociente entre la masa del extremo y la masa total de la soga.

    Esta animación muestra cómo cambian los Kn adimensionales de los modos a partir del caso “analítico” P=0, donde los Kn adimensionales son múltiplos impares de π/2, hasta el caso P=0.3, donde el extremo tiene masa apreciable (casi un tercio de la masa total de la soga).

    Aumentando mucho P, deberíamos encontrar las raíces del seno, no es cierto? Pero por esas cosas de la física computacional, a partir de un cierto valor de P conviene buscar los ceros de

    G(K) = (cos K ) / (K P) + sen (K) ,

    que está servida para dar las raíces del seno cuando P→∞.

    Si llegaste hasta acá, tenés la obligación moral de demostrar todo lo que estuviste leyendo. Y así, estar mejor preparado para luego reflexionar sobre los siguientes puntos:

    • ¿Qué pasa con las series de Fourier que venimos usando hasta ahora?
    • ¿Cuáles son las funciones ortogonales que permiten resolver en forma completa el problema de condiciones iniciales?
    • ¿La evolución temporal es periódica?
    • Observar más abajo la forma de algunos modos (para P=1). ¿Cuántos nodos tiene cada modo? Comparar con los casos “fáciles”. Dar argumentos físicos (es decir, más allá de que “así da la cuenta”) sobre el cambio en la posición de los nodos con el valor del parámetro P.

  • Progresivas y regresivas con perturbaciones localizadas (sin y con velocidad inicial)

    Como en el posteo anterior, se trata de observar cosas curiosas en la evolución de una soga elástica con un extremo fijo y otro libre (sin masa). ¿Sabemos correlacionar esta evolución (que es estacionaria) con los desplazamientos de las ondas viajeras? Para ponernos a prueba, hay que mirar tres animaciones a la vez en cada figura. Y preguntarnos: luego de 7 clases de F2 ¿estamos entendiendo el mundo de las ondas?

    En el primer caso, a t=0 la deformación es gaussiana picuda (no está centrada como en el post anterior, ¿qué cambia?) y sin velocidad inicial.

    El panel superior muestra la solución estacionaria como suma de modos, e incluye como referencia la forma y la velocidad inicial. Los paneles del medio muestran las componentes progre y regre. Y el panel de abajo es la suma, como test (necesario pero no suficiente) de que está todo bien.

    En el segundo ejemplo se muestra algo muy parecido, pero ahora con velocidad inicial localizada en otra parte de la soga.

    A primera vista parece que a veces hay dos progre y a veces ninguna, ídem con la regre. ¿Es raro? ¿Cómo se explica?

    Y en el tercer ejemplo se muestra algo muy parecido, pero ahora son dos pulsitos idénticos localizados inicialmente en los tercios y soltados sin velocidad inicial. ¿Qué les pasa a los pulsitos cuando se juntan? ¿Es cierto que a veces pulsito + pulsito = 0? ¿Qué cambios esperamos cuando los pulsitos no son idénticos?

    (Recordatorio para mi: guardar este post en preferidos para cuando me quedo sin preguntas en un final).

  • Observaciones en una soga con un extremo fijo y otro libre

    Comparen los resultados de estas simulaciones entre si y con la animación anterior con dos extremos fijos.

    La perturbación inicial ya no es un pulso cuadrado (porque calculo las integrales numéricamente y no a mano): tiene la forma del producto de un seno de periodo 2L por una gaussiana centrada en L/2 (curva punteada).

    La velocidad inicial de la cuerda es cero para todo punto como en el caso de la soga con ambos extremos fijos.

    Cuando la perturbación inicial es bastante ancha (gaussiana extendida), el resultado es el siguiente:

    Para una perturbación mucho más localizada, (gaussiana más picuda), el resultado es:

    Tareas a realizar

    • identificar las ondas progresivas y regresivas durante toda la simulación
    • discutir diferencias y semejanzas del comportamiento en los extremos. Explicar matemática y físicamente.
    • cómo cambian los resultados si se imprime velocidad inicial a los puntos de la soga?
    • se podrían definir “coeficientes de reflexión” para los extremos? Si la respuesta es afirmativa, ¿qué valor habría que asignar a estos coeficientes?

  • Armónicos en la guitarra

    Lo más común es que una cuerda de guitarra suene en una combinación de modos que contiene al modo fundamental (con mayor amplitud) y una combinación de modos que depende de cómo fue “tocada” la cuerda. En algunas partituras, los compositores piden explícitamente que se inhiba completamente el modo fundamental y que la cuerda vibre de manera tal que la mayor amplitud en la serie de Fourier sea la de un modo superior determinado. Como se explica en este video, para lograr la inhibición del modo fundamental, el intérprete genera nodos en la condición inicial. Si lo hace en la mitad de la cuerda, entonces genera mayormente el modo 2. Si lo hace a una longitud L/3 del clavijero (o del puente), entonces genera mayormente el modo 3, etc.

  • Evolución de un pulsito

    A discutir mañana: cuerda con extremos fijos, perturbaciòn inicial sin velocidad. Calculado à la Fourier (no à la d’Alembert, otra manera que discutiremos en un par de clases).

  • Animación extremo libre

    Para futura referencia: animación del modo más alto en una cadena con 5 cuentas equiespaciadas, extremo izquierdo fijo y derecho libre (masa cero). 2ω0 es la frecuencia que multiplica al seno en la ecuación de dispersión.

  • Para tener a mano

    Voy a hacer referencia a esto en la clase teórica del viernes 21. Se trata de un código de ejemplo de manejo simbólico (o sea, no numérico) en Python, usando una terminal (en este caso de Windows, símbolo del sistema).

    Copio abajo el código (sin las salidas de los comandos):

    import sympy as sp
    k, K, m = sp.symbols('k K m')
    a = (k + K) / m
    d = (k + K) / m
    b = -k / m
    c = -k / m
    A = sp.Matrix([[a, b], [c, d]])
    autovalores = A.eigenvals()
    autovectores = A.eigenvects()

  • Bienvenidos a la materia

    Bienvenidos a Física 2A. Las clases serán los martes (aula 3, P1) y viernes (aula 2, P1) de 9 a 14. El martes 18 no habrá clases en adhesión a los paros universitarios anunciados.

    El próximo viernes 21 empezamos. Las primeras teóricas serán más largas (9-12) y al comienzo de las prácticas (12-14) se hará un repaso de los temas de Física 1 que consideramos que hay que saber sí o si. Luego de algunas clases con esta distribución horaria, volveremos a la “normalidad”, con teóricas de 9 a 11 y prácticas de 11 a 14.

    ¡Hasta el viernes!

WordPress Appliance - Powered by TurnKey Linux