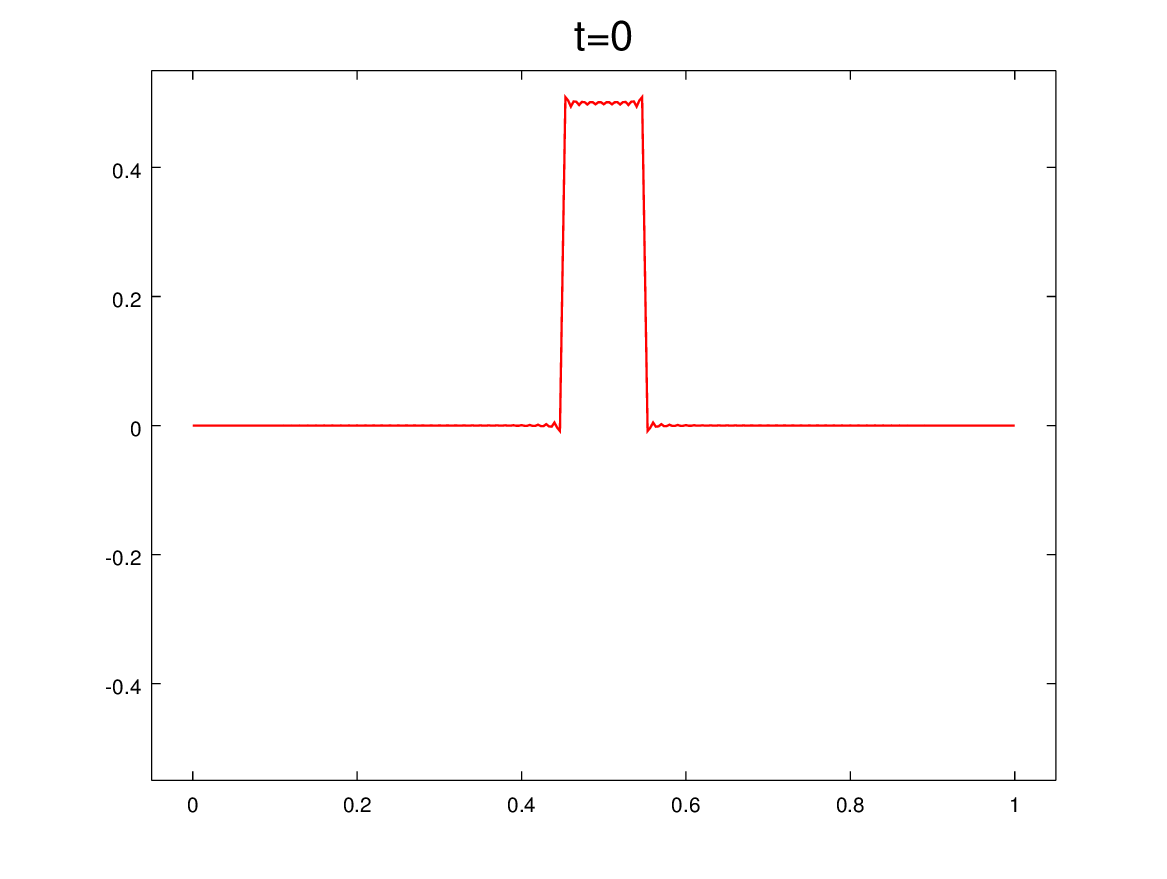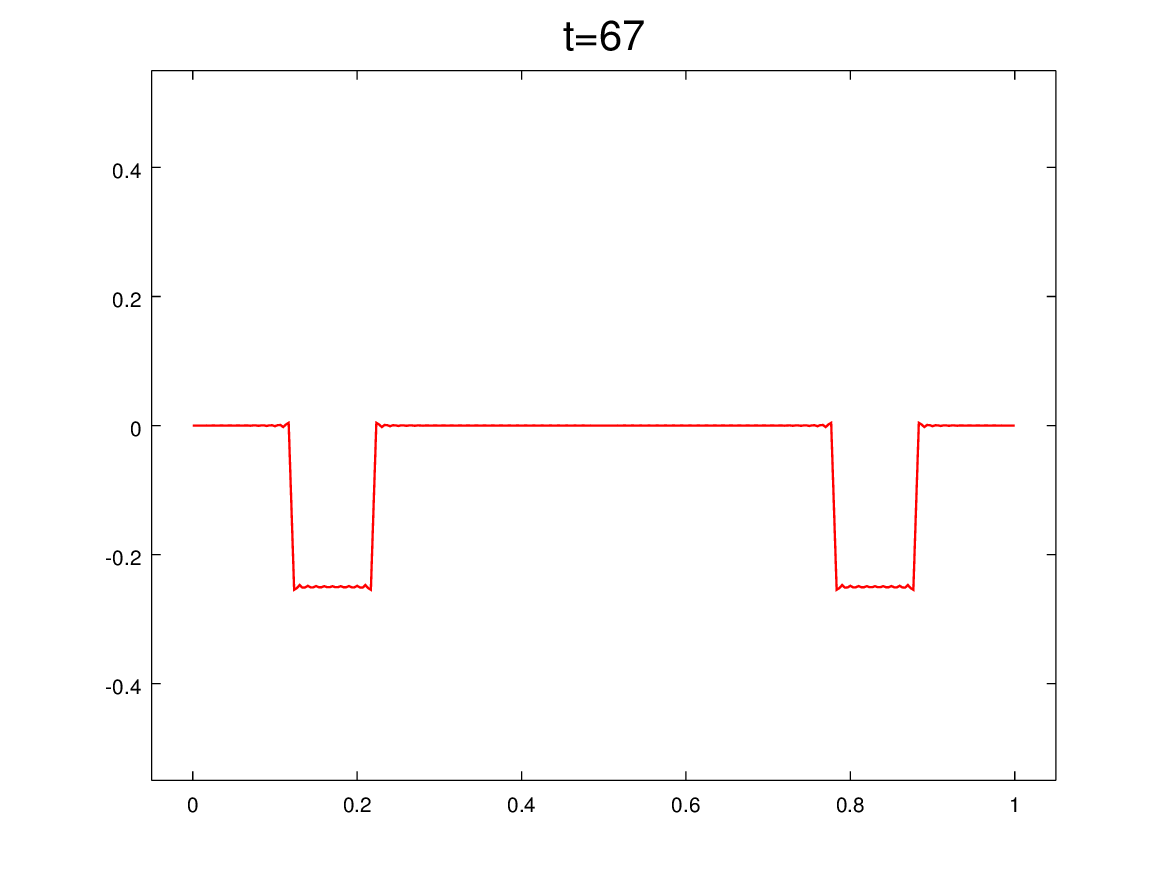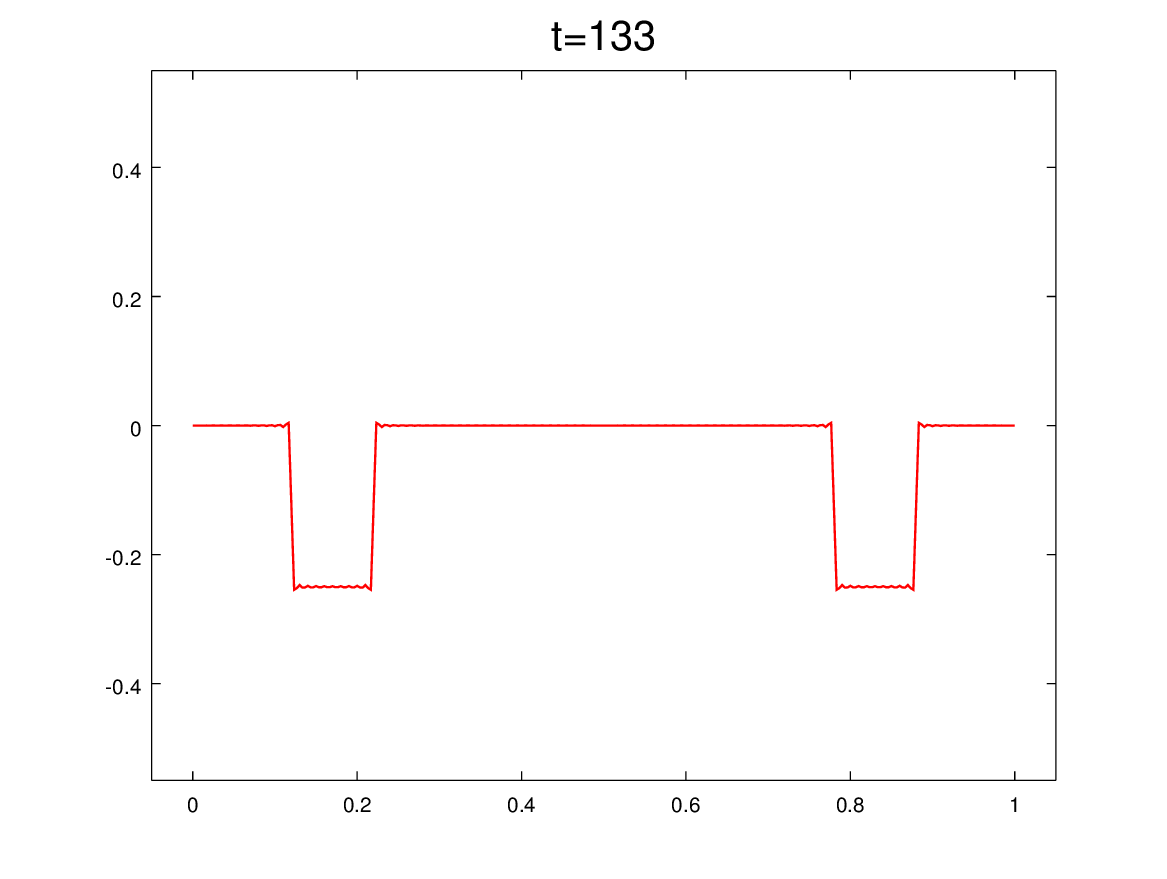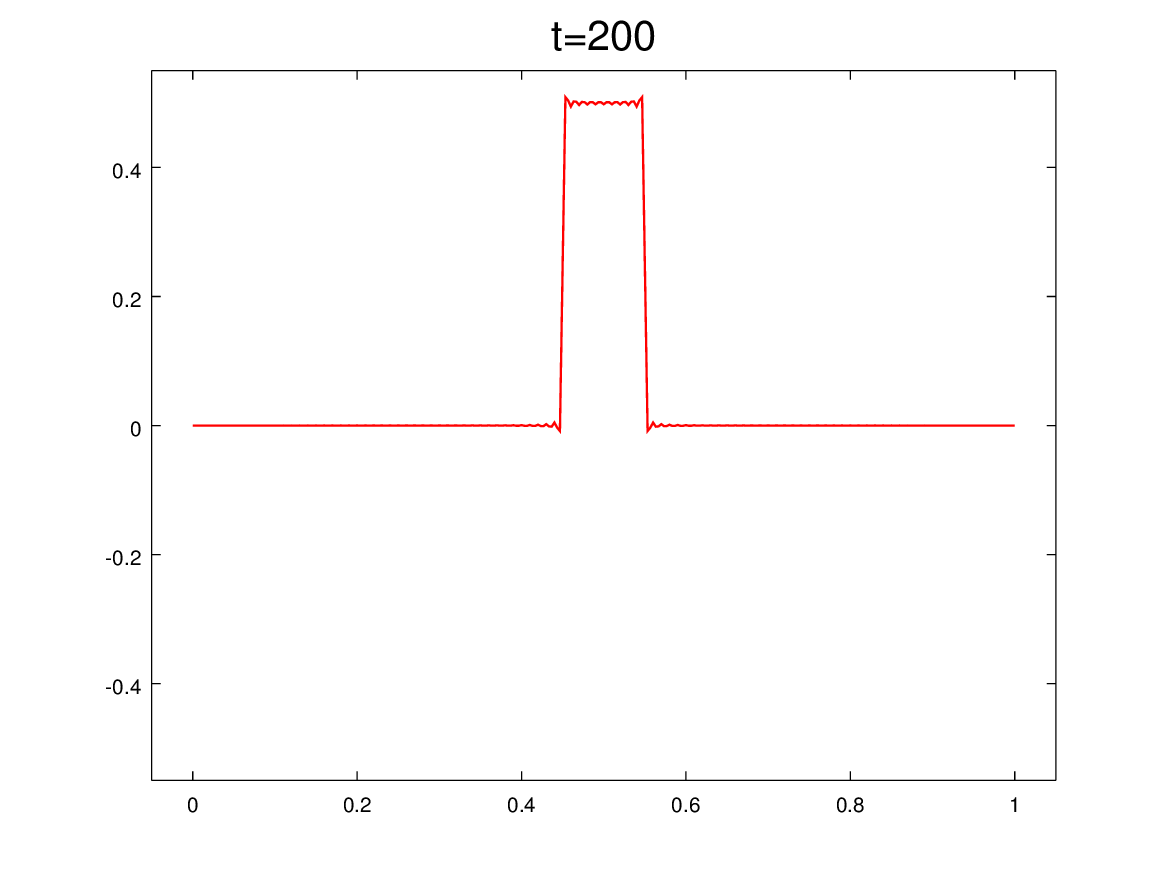
Como en el posteo anterior, se trata de observar cosas curiosas en la evolución de una soga elástica con un extremo fijo y otro libre (sin masa). ¿Sabemos correlacionar esta evolución (que es estacionaria) con los desplazamientos de las ondas viajeras? Para ponernos a prueba, hay que mirar tres animaciones a la vez en cada figura. Y preguntarnos: luego de 7 clases de F2 ¿estamos entendiendo el mundo de las ondas?
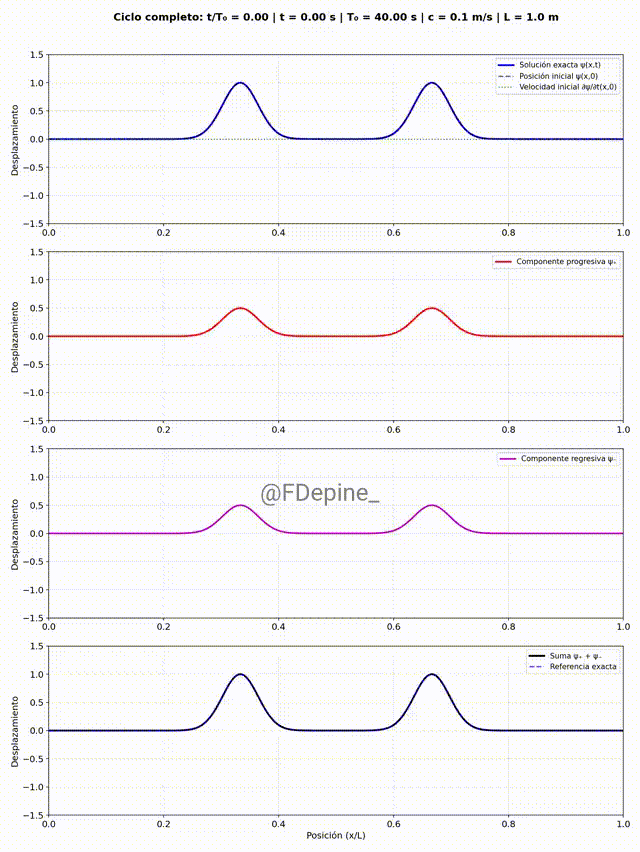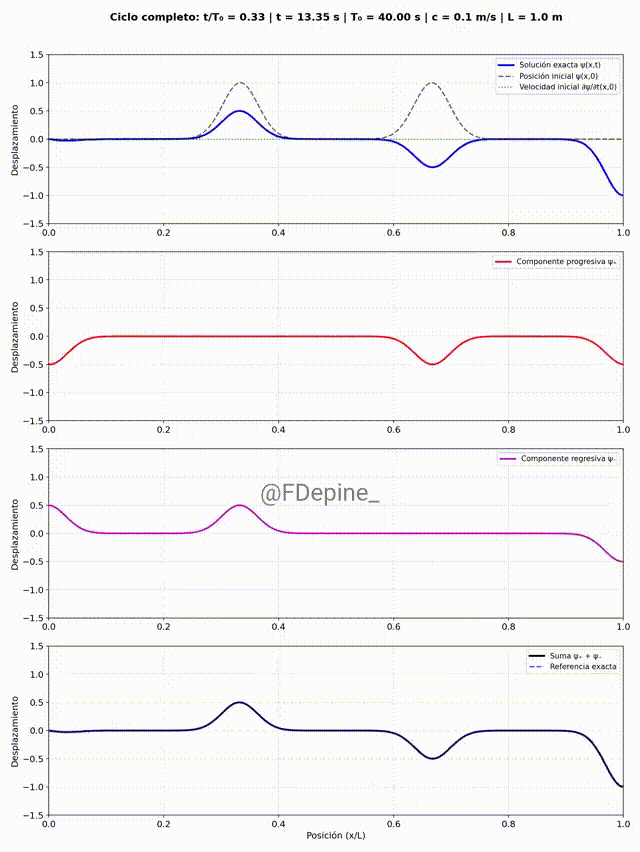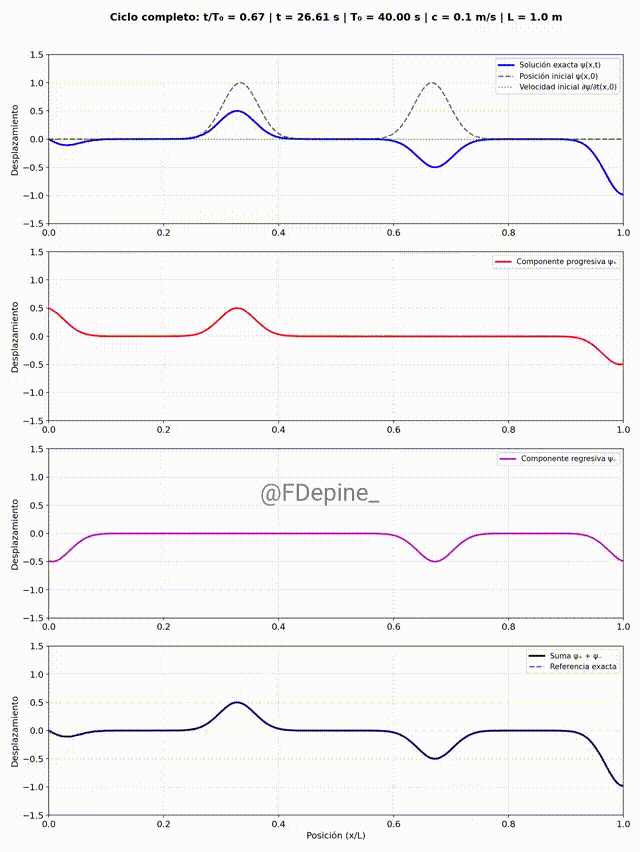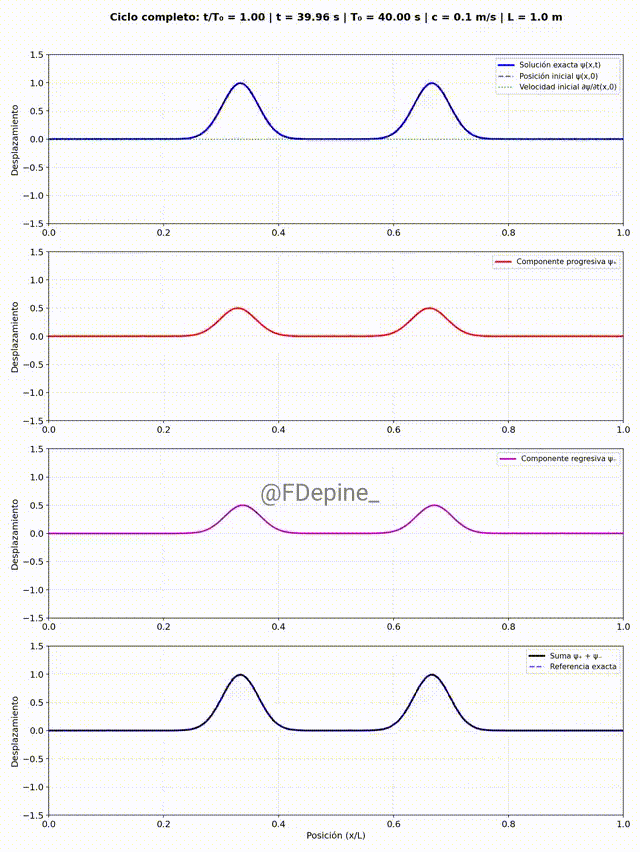
En el primer caso, a t=0 la deformación es gaussiana picuda (no está centrada como en el post anterior, ¿qué cambia?) y sin velocidad inicial.
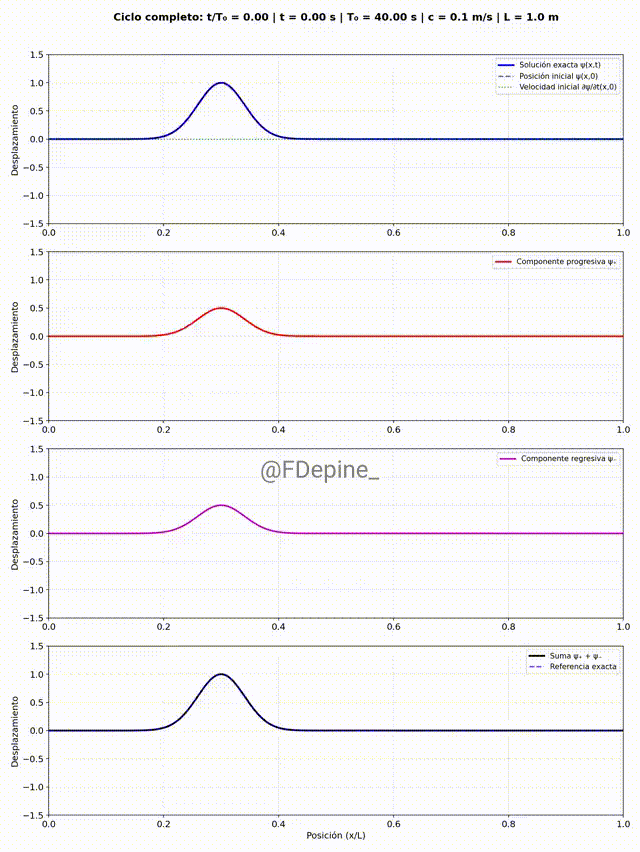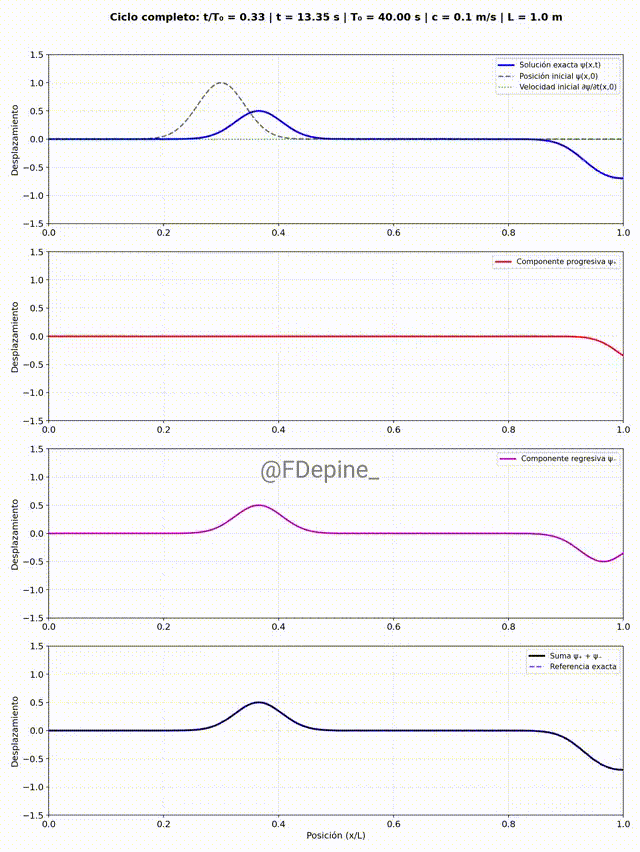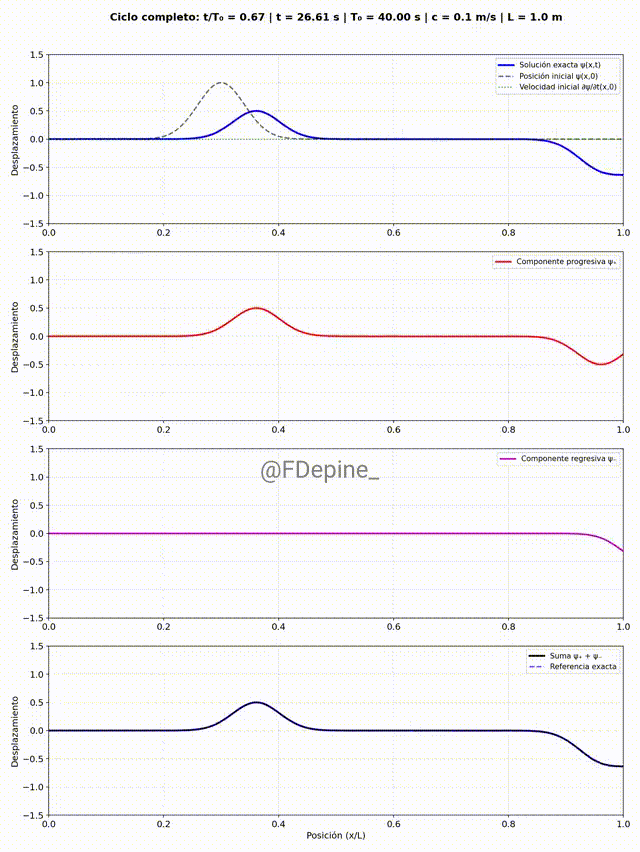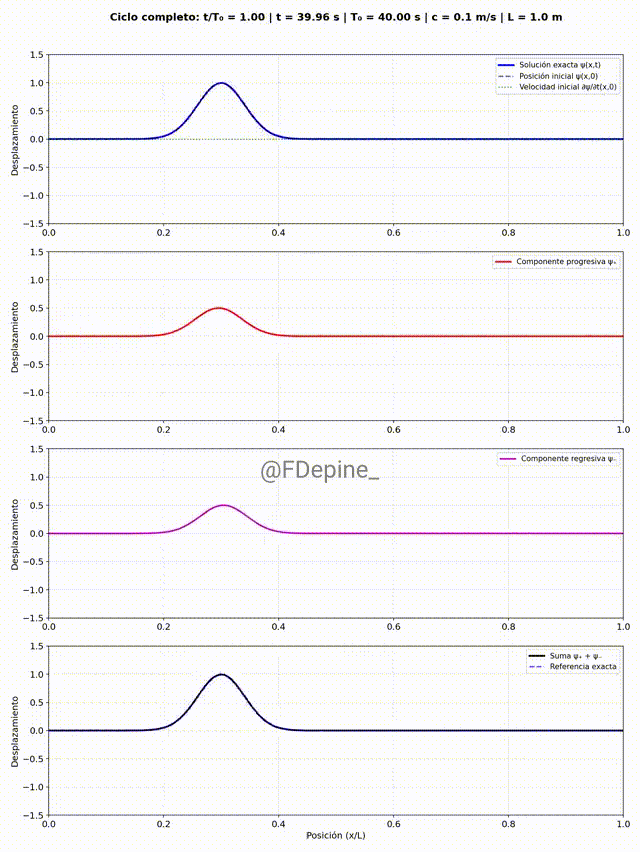
El panel superior muestra la solución estacionaria como suma de modos, e incluye como referencia la forma y la velocidad inicial. Los paneles del medio muestran las componentes progre y regre. Y el panel de abajo es la suma, como test (necesario pero no suficiente) de que está todo bien.
En el segundo ejemplo se muestra algo muy parecido, pero ahora con velocidad inicial localizada en otra parte de la soga.
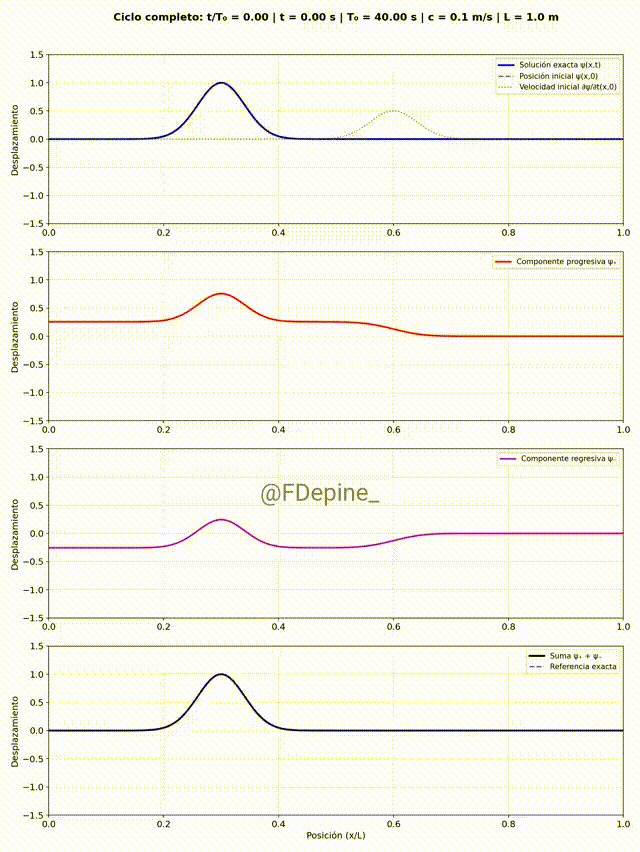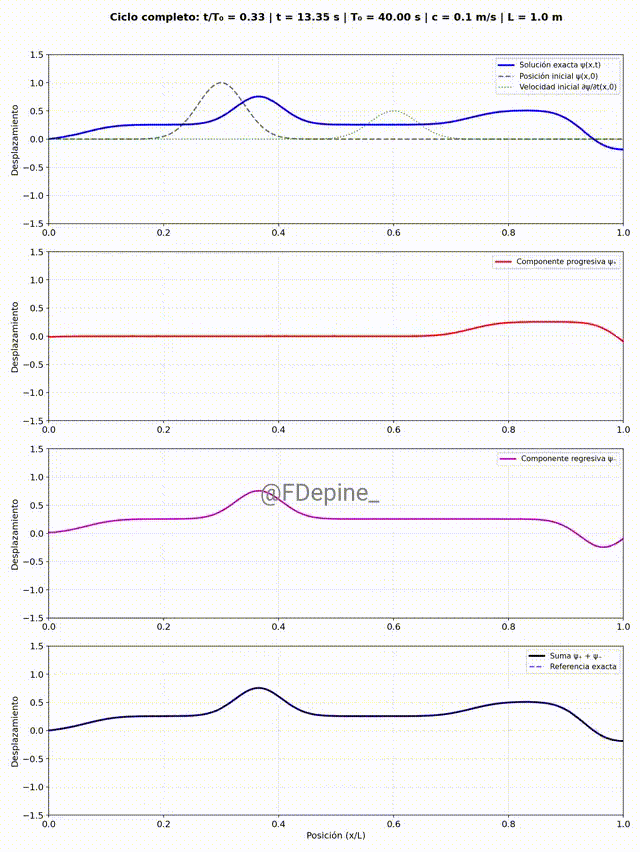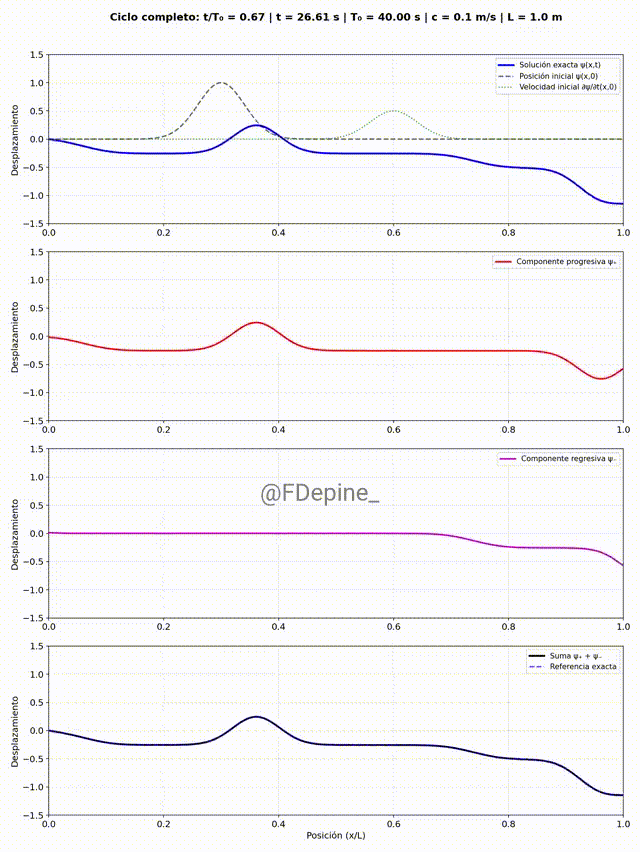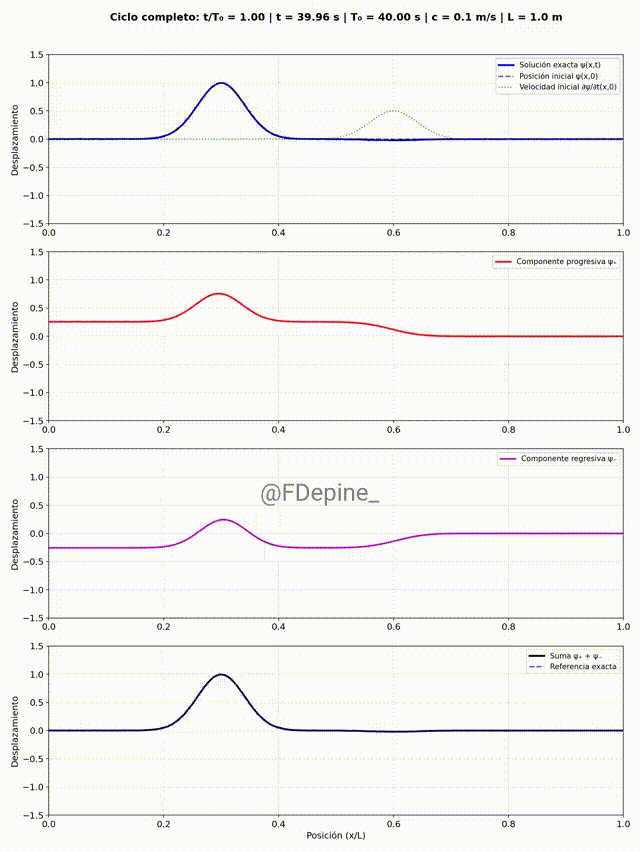
A primera vista parece que a veces hay dos progre y a veces ninguna, ídem con la regre. ¿Es raro? ¿Cómo se explica?
Y en el tercer ejemplo se muestra algo muy parecido, pero ahora son dos pulsitos idénticos localizados inicialmente en los tercios y soltados sin velocidad inicial. ¿Qué les pasa a los pulsitos cuando se juntan? ¿Es cierto que a veces pulsito + pulsito = 0? ¿Qué cambios esperamos cuando los pulsitos no son idénticos?
(Recordatorio para mi: guardar este post en preferidos para cuando me quedo sin preguntas en un final).