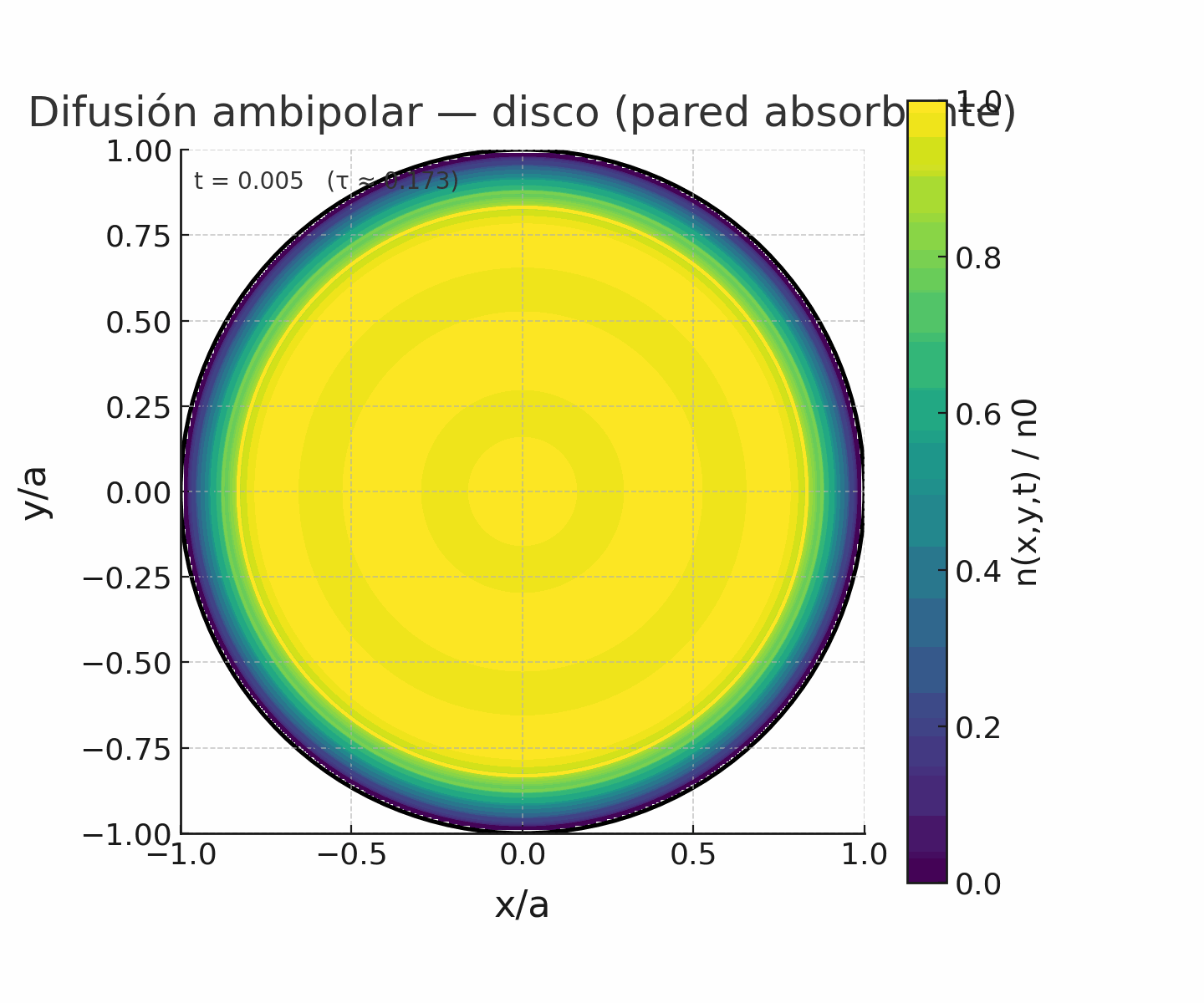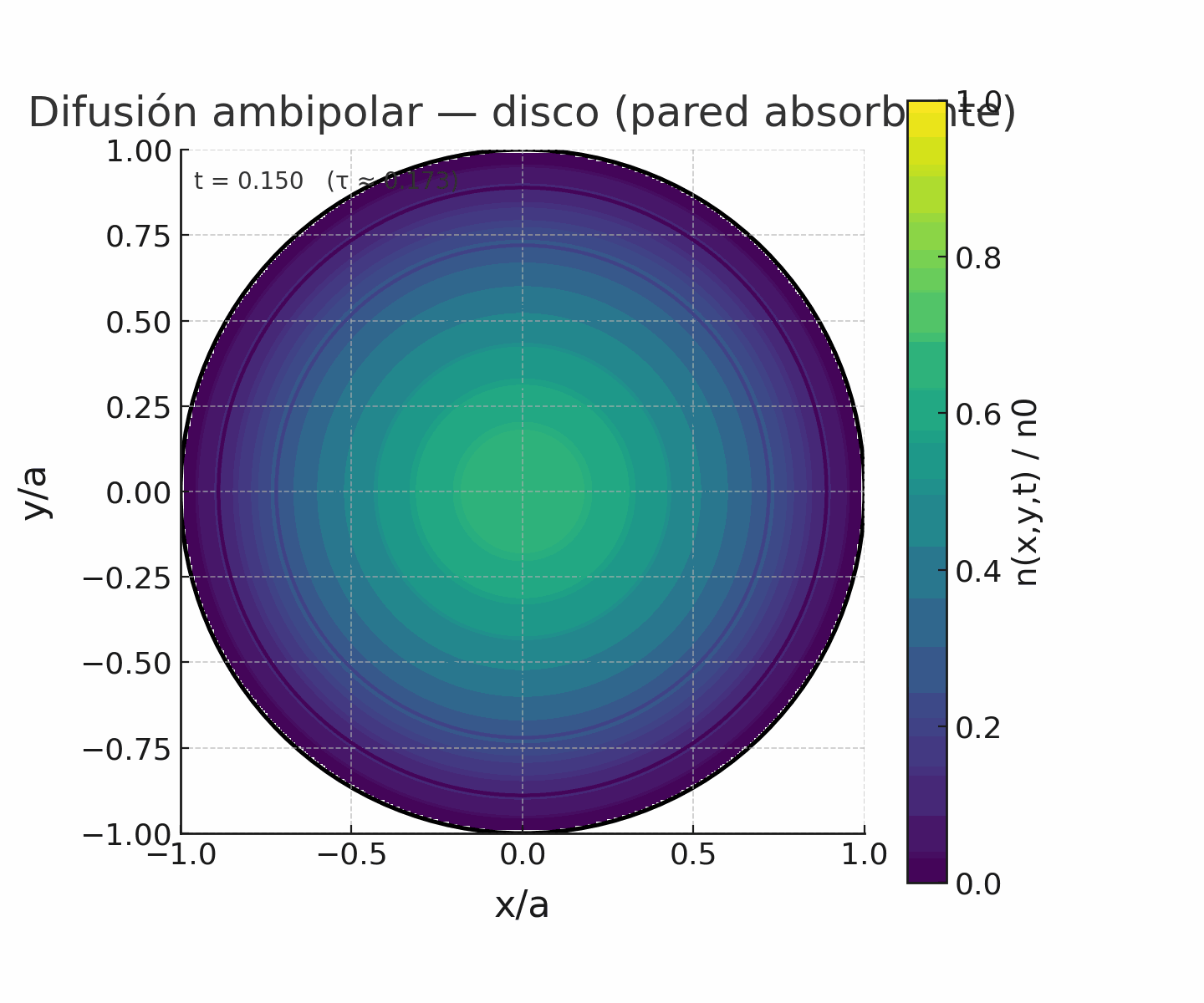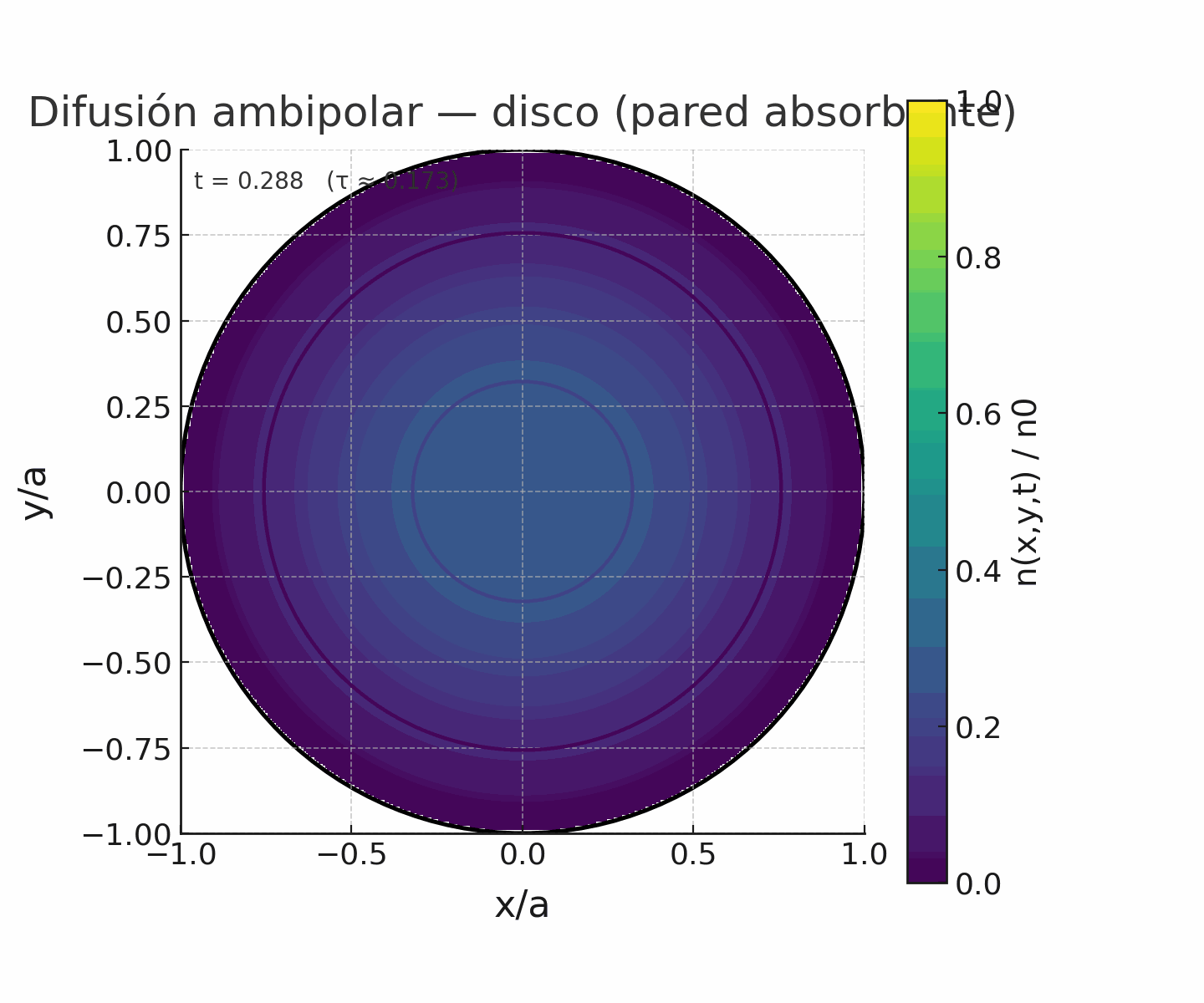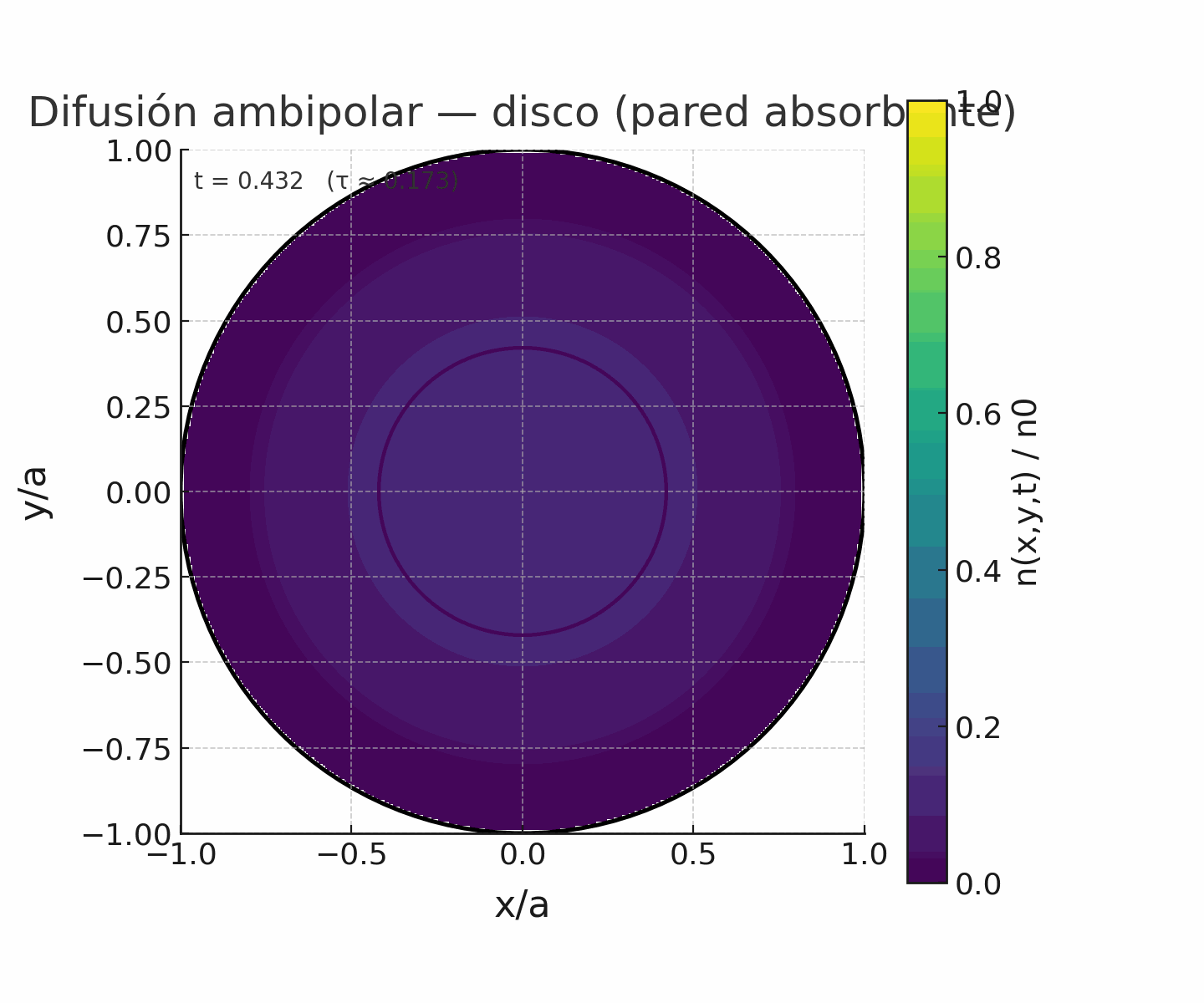
Código de pyhton para simular las líneas de campo helicoidal correspondiente a un equilibrio libre de fuerzas tipo Beltrami con λ cte. (Correr el código en compu, en colab no corre bien el slide)

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jv
from scipy.special import jnyn_zeros
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider
from matplotlib.patches import Arrow, Ellipse
from matplotlib.markers import MarkerStyle
from matplotlib.transforms import Affine2D
Nr = 12
rs = -np.linspace(-12, 0, Nr, endpoint=False)[::-1]
zmax = 20
dtheta = np.pi/20
fig = plt.figure(constrained_layout=True)
#ax = fig.add_subplot(121, projection='3d')
ax = fig.add_axes([-0.3, -0.05, 1.15, 1.1], projection='3d')
#ax.view_init(elev=30, azim=60)
for r in rs:
m = -r*jv(0, r)/jv(1, r)
theta_max = zmax/np.abs(m)
thetas = np.arange(-theta_max, theta_max, dtheta)
z = m*thetas
phase = np.random.random()*2*np.pi
x = r*np.cos(thetas+phase)
y = r*np.sin(thetas+phase)
if (jv(1, r)>0):
ax.plot(x, y, z, "b-", alpha=0.6)
else:
ax.plot(x, y, z, "r-", alpha=0.6)
line, = ax.plot([0,0], [0,0], [-zmax, zmax], "k-")
ax.set_xlim(-21, 21)
ax.set_ylim(-21, 21)
ax.set_zlim(-zmax, zmax)
ax.set_axis_off()
def draw_circle(ax, radius, color, sign):
ellipse = Ellipse(xy=(0, 0), width=2*radius, height=2*radius,
angle=0,facecolor="none", edgecolor=color, lw=2)
ax.add_patch(ellipse)
vertices = ellipse.get_co_vertices()
t = Affine2D().rotate_deg(ellipse.angle)
mkr = ">"*(sign==-1) + "<"*(sign==1)
ax.plot(vertices[0][0], vertices[0][1], color=color,
marker=MarkerStyle(mkr, "full", t), markersize=8)
def draw_spiral(ax, r, sign_z, sign_theta):
N = 100
thetas = np.linspace(0, 2*np.pi, N, endpoint=False)
spiral = []
greys = np.linspace(0.1, 1, N-1)
greys = greys[::-sign_z] # If sign_z == -1, reverse order
rs = r*np.linspace(0.97, 1.03, N-1)[::sign_z]
for i in range(N-1):
c = (greys[i], greys[i], greys[i])
line, = ax.plot(rs[i]*np.cos(thetas[i:i+2]), rs[i]*np.sin(thetas[i:i+2]), "-", color=c, lw=2, zorder=-1)
spiral.append(line)
mkr = "^"*(sign_theta==-1) + "v"*(sign_theta==1)
line, = ax.plot(r*np.cos(thetas[N//2]), r*np.sin(thetas[N//2]), color=(greys[N//2], greys[N//2], greys[N//2]), marker=mkr, ms=8, zorder=-1)
spiral.append(line)
return spiral
ax2 = fig.add_axes([0.5, 0.1, 0.40, 0.9])
ax2.set_aspect(1)
get_roots = lambda n, N: jnyn_zeros(n, N)[0]
M = 4
J0_roots = get_roots(0, M)
J1_roots = get_roots(1, M)
phis = np.linspace(0, 2*np.pi, 1000)
ax2.plot([0], [0], ms=10, marker=r"$\odot$", color=(0,0.4,0))
for r0, r1 in zip(J0_roots, J1_roots):
n = int(np.round(5*r1))
thetas = np.linspace(0, 2*np.pi, n, endpoint=False)
if (jv(0, r1)>0):
ax2.plot(r1*np.cos(thetas), r1*np.sin(thetas), ls="", ms=10, marker=r"$\odot$", color=(0,0.4,0))
else:
ax2.plot(r1*np.cos(thetas), r1*np.sin(thetas), ls="", ms=10, marker=r"$\otimes$", color=(0,0.4,0))
if (jv(1, r0)<0):
draw_circle(ax2, r0, "blue", 1)
else:
draw_circle(ax2, r0, "red", -1)
ax2.set_xlim(-1.15*J1_roots.max(), 1.15*J1_roots.max())
ax2.set_ylim(-1.15*J1_roots.max(), 1.15*J1_roots.max())
spiral = []
ax2.set_axis_off()
ax_r = fig.add_axes([0.25, 0.06, 0.60, 0.05])
r_slider = Slider(ax_r, r'$|\lambda r|$', 0, 15, valinit=0)
r_slider.label.set_fontsize(18)
def update(val):
global spiral
r = r_slider.val
if (r == 0):
line.set_data_3d([0,0], [0,0], [-zmax, zmax])
return
m = -r*jv(0, r)/jv(1, r)
theta_max = zmax/np.abs(m)
thetas = np.arange(-theta_max, theta_max, dtheta)
z = m*thetas
phase = np.random.random()*2*np.pi
x = r*np.cos(thetas+phase)
y = r*np.sin(thetas+phase)
line.set_data_3d(x, y, z)
for L in spiral:
L.remove()
spiral = draw_spiral(ax2, r, int(np.sign(jv(0,r))), -int(np.sign(jv(1,r))))
fig.canvas.draw_idle()
# Connect update function to slider events
r_slider.on_changed(update)