En la clase de hoy hemos discutido la ley de grandes números y el teorema central del límite, en una versión levemente restringida. Al final de la clase les quería mostrar algunos gráficos, pero no lo pude hacer por problemas técnicos. Ahí van.
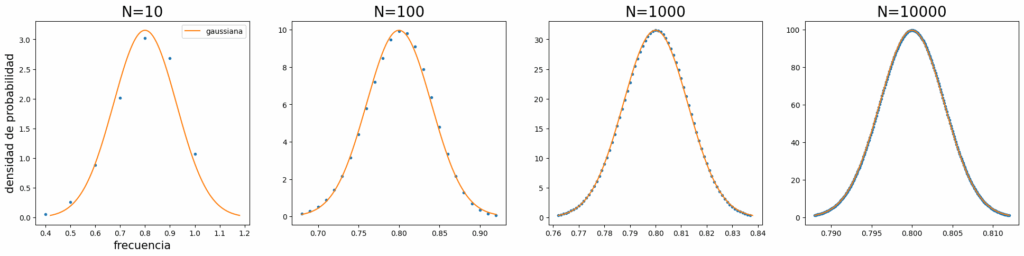
Consideremos un experimento con dos resultados posibles, éxito y fracaso, y supongamos que la probabilidad de éxito es p. Si repito N veces el experimento, la frecuencia (fracción de veces) con que aparece el resultado éxito es una variable aleatoria. En el límite cuando N tiende a infinito, esta variable se vuelve determinista y su valor es p con probabilidad 1. Esto es la ley de grandes números. Acá tienen unos gráficos que permiten visualizar este resultado con p=0.8. A medida que aumenta N, la distribución para la frecuencia se vuelve más y más estrecha.

Si N es muy grande pero no lo mando a infinito, entonces la frecuencia es aproximadamente una variable gaussiana de valor medio p y varianza p(1-p)/N. Esto es el teorema central del límite. Para verlo, comparamos los gráficos anteriores con la gaussiana del teorema, y hacemos zoom cerca del pico para aumentar la resolución.
El colab con el que hice estos gráficos, acá.

Deja un comentario