
[Aquí] pueden bajar la Guía 4, completamente renovada. La respuesta es sí: entra en el parcial.

[Aquí] pueden bajar la Guía 4, completamente renovada. La respuesta es sí: entra en el parcial.
“Ha llegado el momento de anunciar: Esta isla, con sus edificios, es nuestro paraíso privado. He tomado algunas precauciones -físicas, morales- para su defensa: creo que lo protegerán. Aquí estaremos eternamente -aunque mañana nos vayamos- repitiendo consecutivamente los momentos de la semana y sin poder salir nunca de la conciencia que tuvimos en cada uno de ellos.“
Adolfo Bioy Casares, La invención de Morel (1940).
Para cerrar la primera mitad de los temas teóricos de la materia, voy a hacer un último comentario sobre la irreversibilidad en el tiempo en sistemas extensos. El título del posteo hace referencia a Eterno resplandor de una mente sin recuerdos, película de 2004 dirigida por Michel Gondry en base a un guión de Charlie Kaufman. Los interesados en las repeticiones pueden ver también I’m Thinking of Ending Things en Netflix (dirigida por Charlie Kaufman), y Memento o Tenet (estas dos últimas dirigidas por Christopher Nolan). También pueden leer “La invención de Morel” de Adolfo Bioy Casares. Pero sepan que la repetición eterna, como los espejos y la cópula para un heresiarca de Uqbar, es abominable (excepto tal vez para Friedrich Nietzsche). Probablemente nos parezca antinatural justamente porque nunca observamos en la naturaleza que las configuraciones de sistemas extensos se repitan exactamente de la misma forma. Esta observación fue una de críticas que Poincaré y Zermelo, entre otros, realizaron a la teoría estadística de Boltzmann. Imagino que Sísifo también tendría sus objeciones. Y a Dormammu tampoco le deben gustar las repeticiones:
En el teorema H de Boltzmann, su entropía casi siempre crece. Imaginemos un gas que ocupa la mitad de un recinto, separado en dos por un tabique. En un dado instante el tabique se retira, y el gas se expande hasta ocupar todo el recinto (con el consecuente aumento de la entropía). Esta expansión es irreversible. Pero como todas las configuraciones son equiprobables, en algún instante todas las moleculas del gas podrían estar nuevamente en la primera mitad del recinto. Y si en ese preciso instante volvemos a poner el tabique, recuperamos en forma espontánea la primera configuración, que tenía menor entropía. Este posible retorno a una configuración previa fue visto por Poincaré como un problema abominable para la teoría de Boltzmann (aunque más tarde Poincaré se convenció del valor de la teoría y se retractó).
Efectivamente, si el número de configuraciones de un gas es discreto, existe una probabilidad no nula de que vuelva espontáneamente a una configuración previa (o, si las configuraciones son contínuas, de que vuelva a una configuración arbitrariamente cercana a la configuración inicial). Pero el tiempo necesario para volver a encontrar esta configuración es increíblemente largo, lo que vuelve a este escenario irrelevante a fines prácticos. Estimemos esto para un metro cúbico de aire a temperatura ambiente (T = 300 K). Vimos que el número de configuraciones Σ de un gas ideal lo podemos calcular, en el ensamble microcanónico, como
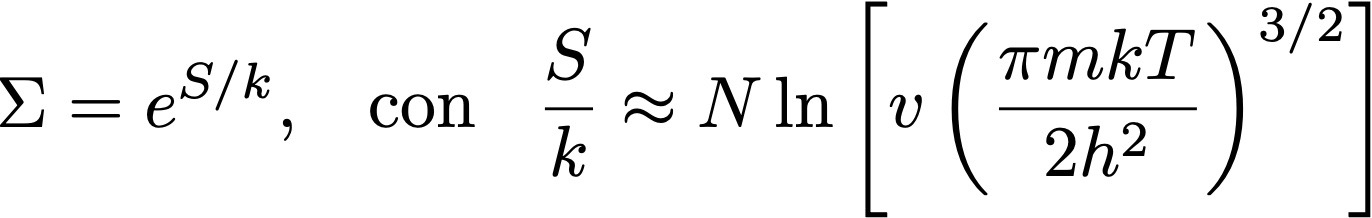
donde S es la entropía, N el número de partículas, v el volúmen específico del gas, m la masa de las partículas (mayormente moléculas de N2), k la constante de Boltzmann, y h la constante de Planck (ignoro un factor aditivo despreciable en la entropía). Usando valores típicos para estos parámetros (y considerando que v ≈ 5 x 10-29 m3), obtenemos que el número de microestados o configuraciones posibles es
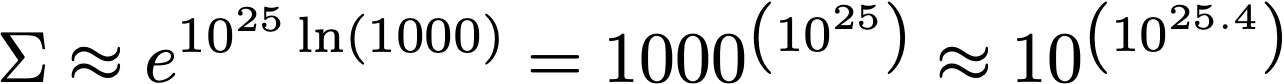
¡Este es un número enorme, con más de 1025 dígitos! Asumamos ahora que las configuraciones cambian cada vez que hay un choque entre partículas. Es decir, cuando las partículas en el gas chocan, intercambian momento, y pasan de una configuración a otra. Como vimos en clase, para el aire a temperatura y presión ambiente, el tiempo entre choques es τ ≈ 10-10 s. Y si todas las configuraciones son equiprobables, podemos estimar el tiempo medio para repetir una configuración como proporcional a Σ·τ, que sigue siendo un número muy grande (un tiempo con más de 1025 dígitos, medido en segundos). ¡Como comparación, la edad del universo es de 4.3 x 1017 s, muchísimo más chica que el tiempo medio necesario para repetir la configuración de un gas en solo un metro cúbico! Por lo que el “casi siempre crece” de Boltzmann está bastante bien. En otras palabras, en sistemas extensos, las chances de que un sistema vuelva en forma espontánea a una configuración previa realmente es despreciable.
Hoy sabemos que aún en sistemas no tan grandes, fuera del equilibro la probabilidad de que la entropía crezca es mucho más grande que la probabilidad de que la entropía disminuya. De hecho, sabemos que la razón entre estas dos probabilidades es igual a la exponencial de la variación de la entropía por el tiempo transcurrido, un número que se vuelve exponencialmente más grande a medida que la entropía del sistema crece, o que transcurre más tiempo. En el caso general, este resultado se conoce como el teorema de fluctuación detallado. Los que quieran aprender más sobre resultados para sistemas fuera del equilibrio pueden leer también sobre el teorema de fluctuación de Crooks, la igualdad de Jarzynski, y las relaciones de Green-Kubo.

Jorge subió un apunte en el Campus con los problemas que vimos hoy en la clase de práctica. En lugar de consultar al irresponsable chatg**, consulten con nosotros a través del Campus.

[Aquí] pueden bajar la clase práctica de ayer. En la guía, hay otros tres problemas similares; en [este] recuperatorio hay otro más. El apunte fue terminado hoy justo a tiempo por un equipo de 1023 monos en tan solo 1045000 años, eones más, eones menos. No pidan que además esté todo bien. Al principio fue un poco lento, porque los monos tenían que confiar lo escrito, por así decirlo, a su memoria. Con las tablas de arcilla adelantamos unos caracteres. En un momento probamos la máquina de pensar de Raimundo Lulio, pero, entre muchas insensateces, al final pensó que no servía para nada.
En la clase de ayer vimos el teorema del virial. Este es un teorema muy útil, tanto en la versión de Mecánica Estadística como en su versión de Mecánica Clásica. Pero también es un teorema que puede ser fácilmente aplicado a situaciones en las que no se cumplen sus hipótesis, para darnos resultados erróneos. Recuerden que las partículas en el sistema deben estar confinadas por el potencial. A continuación les doy dos ejemplos de aplicaciones, que mencioné brevemente en clase.
Comencemos con el gas ideal. Hemos visto que el teorema del virial puede escribirse como
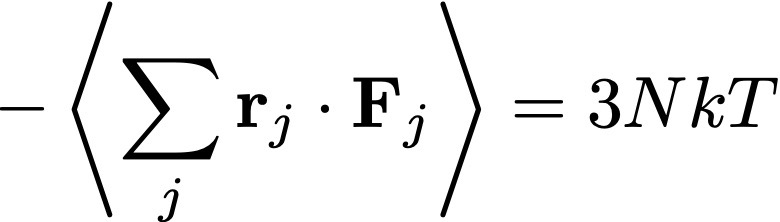
donde las coordenadas r son las posiciones de las partículas, F son las fuerzas sobre cada partícula, N es el número de partículas, y T la temperatura. La suma es sobre todas las partículas. Para un gas ideal, la única fuerza que tenemos está asociada a la presión P. Usando que la fuerza total, sumada sobre todas las partículas, es ∑ r · F = – ∫ r · n P dA (donde n es la normal externa a la pared, y dA el diferencial de superficie), después de hacer algunas cuentas se puede llegar (usando el teorema de Gauss) a que el término de la izquierda es 3PV (con V el volúmen). ¡Por lo que recuperamos la ecuación de estado de un gas ideal: PV = NkT!
Veamos ahora una aplicación más interesante. Consideremos un clúster de N galaxias (es decir, una acumulación de galaxias en el universo), cada una con masa m y con masa total M = Nm. Por ejemplo, podría ser el cúmulo de Coma, un clúster con más de 1000 galaxias identificadas a 321 millones de años luz de la Tierra:

Las galaxias en el clúster están confinadas por la fuerza gravitatoria. Nos conviene ahora escribir el teorema del virial, para una fuerza que decae como el cuadrado de la distancia, como
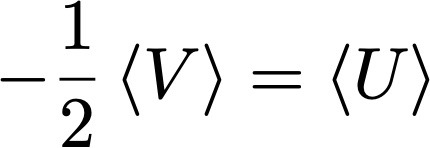
donde U es la energía cinética y V ahora es la energía potencial. Asumiendo que el clúster es esférico, para la fuerza gravitatoria V = -3GM 2/(5R), donde G es la constante de gravitación universal, y R el radio del clúster. Por otro lado la energía cinética media es <U > = M <v 2>/ 2. De estas dos relaciones podemos estimar la masa del clúster como
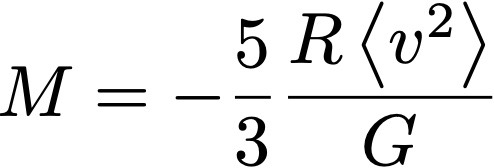
La velocidad cuadrática media de las galaxias en el clúster se puede medir, por ejemplo, por corrimiento Doppler. Y la masa del clúster se puede estimar de forma independiente a esta fórmula a partir de la luminosidad del clúster, usando relaciones bien calibradas en astronomía. Y aquí comienzan los problemas: la fórmula obtenida con el teorema del virial da una masa M mayor que la que se estima con la luminosidad, sugiriendo que falta una fracción de materia que no estamos observando cuando miramos la luminosidad de las galaxias. Este argumento puede ser ampliado para considerar otras formas de energía (por ejemplo, la energía en el campo magnético de las galaxias y del clúster), pero esto no cambia el resultado central: hay una diferencia significativa en la masa estimada por diferentes medios.
Para el caso particular del clúster coma, los primeros estudios que indicaron esta discrepancia entre las masas estimadas de diferentes formas fueron realizados por Fritz Zwicky en 1933. Más tarde, Vera Rubin estudió en detalle la curva de rotación de galaxias individuales, y luego de estudios muy exhaustivos para muchas galaxias, encontró una discrepancia entre la dependencia radial de la velocidad de rotación esperada y la observada, indicando nuevamente una discrepancia entre la masa esperada y la masa observada. Los trabajos de Vera Rubin pusieron en claro la existencia de un problema en cosmología que continúa abierto hasta nuestros días.

Si bien estos no son los únicos argumentos a favor de la existencia de materia oscura, en conjunto con otros resultados nos indican que cerca del 85% de la materia en el universo tiene que ser materia oscura. Y para el caso particular del cúmulo de Coma, estimaciones usando mediciones astronómicas y el teorema del virial indican que cerca del 90% de la materia en el cúmulo es materia oscura.

Así podría empezar mi CV. Pero se trata, en realidad, de un [apunte] con el problema de los defectos de Frenkel que vimos durante la clase de ayer. Y hoy usted se lleva además un [apunte] con el método del término máximo y un [parcial] resuelto que incluye un problema sobre defectos de Frenkel. La oferta se completa con un [apunte] sobre el sistema de los dos niveles que resolvimos la semana pasada. Son apuntes del segundo cuatrimestre de 2024.
En esta escena que mencioné ayer en clase de la película El lobo de Wall Street, dirigida por Martin Scorsese, Matthew McConaughey habla la “fugacidad” de la bolsa de valores. Llamativamente, la lírica de la canción “Money“, de Pink Floyd (del disco The Dark Side of the Moon, tiene la memorable frase “Money, it’s a gas“. Y ninguna de estas frases es simplemente una licencia poética. En muchos sentidos hay conexiones profundas entre la mecánica estadística y el modelado de los mercados bursátiles, que en algunos casos se remontan hasta los inicios de la teoría.
Los que tengan curiosidad sobre cómo se usan herramientas de mecánica estadística para el estudio de economía y finanzas pueden mirar este muy buen review:
que fue publicado en Reviews of Modern Physics en 2009. El artículo es introductorio y explica varios de los conceptos que se usan comúnmente en el área de econofísica, incluyendo modelos estocásticos (como los modelos de camino al azar que vimos en clase), cómo se usan el ensamble canónico y el gran canónico, los vínculos asociados a la “conservación del dinero”, o los vínculos que se usan en sistemas más realistas en los que pueden existir deudas y cómo esto resulta en diferentes equilibrios estadísticos. En particular, la Sección I, y la Sección II desde la subsección A hasta la C, se leen fácilmente y usan muchos de los conceptos que introdujimos hasta ahora en la materia.
En las secciones II.B y II.C, los autores reemplazan el vínculo sobre la energía que usamos al derivar los ensambles, por un vínculo sobre el dinero total circulante. Si asumimos que el dinero total se conserva, la distribución de probabilidad de equilibrio para el dinero está dada por la distribución de Boltzmann-Gibbs,
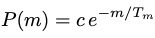
donde m es la cantidad de dinero, y Tm es la “temperatura estadística” del sistema (es decir, el multiplicador de Lagrange asociado al vínculo). Esta cantidad (Tm) es igual al dinero medio disponible por persona. Noten que esta expresión para la probabilidad es formalmente igual a la obtenida en el ensamble canónico. Excepto por casos con ingresos extremadamente grandes (que deben ser modelados con otra distrubución de probabilidad, la distribución de Pareto), la distribución de Boltzmann-Gibbs está en buen acuerdo con los datos de muchos países. A modo de ejemplo, el review compara este resultado con la probabilidad acumulada en función de los ingresos de los individuos usando datos de la oficina de impuestos de los Estados Unidos:
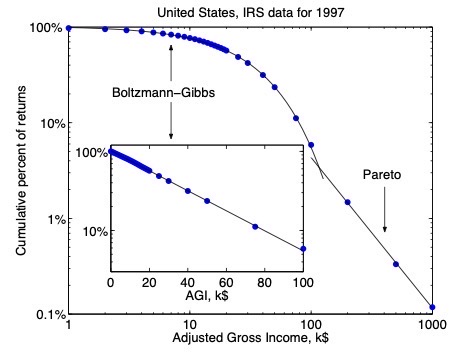
En esta figura los puntos azules son datos (porcentaje acumulado de casos en función de los ingresos brutos ajustados de cada contribuyente), y la linea negra de la izquierda corresponde a la distribución de Boltzmann-Gibbs (o la distribución canónica), seguida por la distribución de probabilidad de Pareto.
Este artículo tiene también un hallazgo interesante sobre la visión amplia que tenía Boltzmann de la física, que más de 100 años atrás vislumbró la aplicabilidad de la mecánica estadística tanto en física como en otras áreas muy diversas del conocimiento (una visión que se cumplió con creces). En 1905 Boltzmann, hablando sobre la generalización y formalización de la mecánica estadística realizada por Gibbs, escribió:
“Esto abre una perspectiva amplia, si no pensamos solamente en objetos mecánicos. Consideremos aplicar este método a la estadística de seres vivos, de la sociedad, en sociología, etc.”
Boltzmann tomó algunas ideas de estadística que ya se aplicaban en su época en el estudio de la sociedad para construir su teoría de los gases diluidos. Así que su propuesta de aplicar la incipiente mecánica estadística en estudios de la sociedad y en sociología podría resultar esperable. La famosa novela de ciencia ficción “Fundación“, de Isaac Asimov, también juega con la idea de aplicar la teoría de gases diluidos en las ciencias sociales para predecir el posible desarrollo de una sociedad. Y las aplicaciones actuales de la mecánica estadística en biología, economía y otras ciencias pueden resultar aún más sorprendentes que lo que imaginaron Boltzmann o Asimov.

La Guía 3 se puede bajar [aquí]. Es La Guía del primer parcial. Abandonen todo lo que estaban haciendo y empiecen a resolver los problemas de esta guía. ¿Qué es un problema por día? Nada. ¿Qué son dos problemas por día? Menos que nada. Un diferencial hoy, un diferencial mañana, cuando se quieren acordar, ya calcularon una integral. Algunos problemas tienen detalles técnicos que recién vamos a ver la semana que viene. Pero con lo que ya vieron en la teórica pueden hacer los problemas del 8 al 11 y con lo que vamos a ver hoy en la práctica, pueden hacer los problemas 1, 2, 7 y 22.
Como mencioné varias veces en el aula, en esta materia no vamos a demostrar ni a derivar la termodinámica. Esta materia es, en cierto sentido, una materia sobre jerarquías en la naturaleza. No siempre podemos derivar un comportamiento complejo como resultado directo de leyes fundamentales. Muchas, muchísimas veces, al trabajar con sistemas complejos o extensos, necesitamos hacer aproximaciones e introducir conceptos que (aunque tienen vínculos con las leyes fundamentales de la naturaleza) tienen sentido solo en forma aproximada (¡como el calor!). Justamente en este video Feynman dice (en el minuto 0:22): “For example, at one end we have the fundamental laws of physics. Then we invent other terms for concepts which are approximate, which have, we believe, their ultimate explanation in terms of the fundamental laws. For instance, ‘heat’. Heat is supposed to be the jiggling, and the word for a hot thing is just the word for a mass of atoms which are jiggling.” (“Por ejemplo, en un extremo tenemos las leyes fundamentales de la física. Luego inventamos otros términos para conceptos que son aproximados, que, creemos, tienen su explicación última en términos de las leyes fundamentales. Por ejemplo, el “calor”. Se supone que el calor es la vibración, y la palabra para algo caliente es solo la palabra que usamos para una masa de átomos que se sacuden.”).
Noten que Feynman no intenta convencernos de que hay una expresión formal y correcta para el calor en términos de leyes o magnitudes físicas fundamentales. Nos dice que el calor es un concepto aproximado para describir ciertos fenómenos en una escala macroscópica. Muchos conceptos en termodinámica son de este tipo: algunos podremos formalizarlos, para otros necesitaremos muchas aproximaciones. Y la descripción microscópica que estamos construyendo será compatible (por diseño y construcción) con la termodinámica, porque si la violase construiríamos otra teoría microscópica. El enfoque de esta materia nos puede ayudar a entender ciertos sistemas físicos de otra forma, pero no se confundan y piensen que porque una teoría se deriva con más cuentas y trabajo es necesariamente mejor. Porque es imposible unir las dos descripciones (la macroscópica y la microscópica) sin hacer muchas aproximaciones en el medio.
Sobre este punto, en el video Feynman dice algo muy interesante, y que va contra la concepción simplista de la física que imagina que entender un fenómeno se reduce siempre a reducirlo a las leyes o principios fundamentales que están detrás. En el video Feynman continúa hablando de sistemas cada vez mas complejos, y aproximaciones cada vez mayores. Y en el minuto 2:52 se pregunta: “Which end is nearer to the ultimate creator, if I may use a religious metaphor? Which end is nearer to God? Beauty and hope, or the fundamental laws? I think that the right way, of course, is to say that the whole structural interconnection of the thing is what we have to look at. […] And so I do not think either end is nearer to God. To stand at either end, and to walk off that end of the pier only, hoping that out in that direction is the complete understanding, is a mistake.” (“¿Qué extremo está más cerca del creador final, si puedo usar una metáfora religiosa? ¿Qué extremo está más cerca de Dios? ¿La belleza y la esperanza, o las leyes fundamentales? Creo que la respuesta correcta, por supuesto, es decir que lo que debemos mirar es la interconexión completa de las cosas. […] Y entonces no creo que ninguno de los dos extremos esté más cerca de Dios. Pararse en cualquier extremo y caminar solo por ese extremo del muelle, esperando que partiendo desde ese punto encontraremos el entendimiento completo, es un error.”).
En términos más contemporáneos, los sistemas físicos extensos son como los ogros. Y los ogros son como las cebollas. ¿Apestan? ¡No! ¿Te hacen llorar? ¡No! ¿Si los dejás al sol se vuelven marrones y les crecen pelitos blancos? ¡Tampoco! Las cebollas tienen capas. Los ogros tiene capas. Y los sistemas físicos extensos tienen capas, como los ogros y las cebollas.

Y como los ogros, los sistemas físicos extensos no pueden comprenderse si solo miramos las capas más externas, o si solo miramos las capas centrales.
Para los que quieran aprender más sobre la visión de Feynman sobre cómo se construyen las leyes físicas, el video que está arriba es un extracto de una serie de siete seminarios que Feynman dio en Cornell, con el título “The character of physical law“. Pueden encontrar los videos de sus seminarios online, y también fueron transcriptos a un libro.